7．某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查，得到的统计数据如下表所示：
（Ⅰ）如果随机调查这个班的一名学生，那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少？
（Ⅱ）若不积极参加班级工作且学习积极性高的7名学生中有两名男生，现从中抽取两名学生参加某项活动，问两名学生中有1名男生的概率是多少？
（Ⅲ）学生的积极性与对待班级工作的态度是否有关系？请说明理由．
附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| 积极参加班级工作 | 不积极参加班级工作 | 合计 | |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性不高 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
（Ⅱ）若不积极参加班级工作且学习积极性高的7名学生中有两名男生，现从中抽取两名学生参加某项活动，问两名学生中有1名男生的概率是多少？
（Ⅲ）学生的积极性与对待班级工作的态度是否有关系？请说明理由．
附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| p（K2≥k0） | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
5．若定义域为D的函数f（x）满足：
①f（x）在D内是单调函数；
②存在[a，b]⊆D，使得f（x）在[a，b]上的值域为[$\frac{a}{2}$，$\frac{b}{2}$]，则称函数f（x）为“半值函数”．
已知函h（x）=logc（cx+t）（c＞0，c≠1）是“半值函数”则实数t的取值范围为（ ）
①f（x）在D内是单调函数；
②存在[a，b]⊆D，使得f（x）在[a，b]上的值域为[$\frac{a}{2}$，$\frac{b}{2}$]，则称函数f（x）为“半值函数”．
已知函h（x）=logc（cx+t）（c＞0，c≠1）是“半值函数”则实数t的取值范围为（ ）
| A． | （0，+∞） | B． | （-∞，$\frac{1}{4}$） | C． | （$\frac{1}{4}$，+∞） | D． | （0，$\frac{1}{4}$） |
4．设{an}是等比数列，则对任何n∈N*，都有$\frac{1}{{{a_1}{a_2}}}•\frac{1}{{{a_2}{a_3}}}…\frac{1}{{{a_n}{a_{n+1}}}}$=（ ）
| A． | $\frac{1}{{{{（{a_1}•{a_n}）}^n}}}$ | B． | $\frac{1}{{{{（{a_1}•{a_{n+1}}）}^n}}}$ | C． | $\frac{1}{{{{（{a_1}•{a_n}）}^{n+1}}}}$ | D． | $\frac{1}{{{{（{a_1}•{a_{n+1}}）}^{n+1}}}}$ |
19．
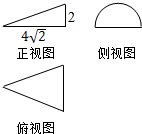一个几何体的三视图及尺寸如图所示，其中正视图是直角三角形，侧视图是半圆，俯视图是等腰三角形，该几何体的体积为（ ）
0 246767 246775 246781 246785 246791 246793 246797 246803 246805 246811 246817 246821 246823 246827 246833 246835 246841 246845 246847 246851 246853 246857 246859 246861 246862 246863 246865 246866 246867 246869 246871 246875 246877 246881 246883 246887 246893 246895 246901 246905 246907 246911 246917 246923 246925 246931 246935 246937 246943 246947 246953 246961 266669
一个几何体的三视图及尺寸如图所示，其中正视图是直角三角形，侧视图是半圆，俯视图是等腰三角形，该几何体的体积为（ ）| A． | $\frac{8\sqrt{2}π}{3}$ | B． | $\frac{16\sqrt{2}π}{3}$ | C． | 4$\sqrt{2}π$ | D． | 8$\sqrt{2}π$ |