题目内容
3.已知Sn是等比数列{an}的前n项和,若S2=1,S4=3,则S8=15.分析 利用等比数列的通项公式与前n项和公式即可得出.
解答 解:设等比数列{an}的公比为q,显然q≠1,${S_2}=\frac{{{a_1}(1-{q^2})}}{1-q}=1$,${S_4}=\frac{{{a_1}(1-{q^4})}}{1-q}=3$,
由$\frac{S_4}{S_2}=3$得q2=2,
∴${S_8}=\frac{{{a_1}(1-{q^8})}}{1-q}=\frac{{{a_1}(1-{q^2})}}{1-q}(1+{q^2})(1+{q^4})=15$.
故答案为:15.
点评 本题考查了等比数列的通项公式与前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
13.已知正四棱柱底面边长为1高为2,俯视图是一个面积为1的正方形,则该正四棱锥的正视图的面积不可能等于( )
| A. | 2 | B. | 2.5 | C. | 2$\sqrt{3}$-1 | D. | 2$\sqrt{2}$+1 |
14.设min{p,q}表示p,q两者中的较小者,若函数f(x)=min{3-x,log2x},则满足f(x)≤$\frac{1}{2}$的x的集合为( )
| A. | (0,2]∪[$\frac{5}{2}$,+∞) | B. | [$\sqrt{2}$,$\frac{5}{2}$] | C. | (0,$\sqrt{2}$]∪[$\frac{5}{2}$,+∞) | D. | (0,$\sqrt{2}$)∪($\frac{5}{2}$,+∞) |
18. 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为得到g(x)=cosωx的图象,则只要将f(x)的图象( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为得到g(x)=cosωx的图象,则只要将f(x)的图象( )
 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为得到g(x)=cosωx的图象,则只要将f(x)的图象( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,为得到g(x)=cosωx的图象,则只要将f(x)的图象( )| A. | 向右平移$\frac{π}{6}$个单位长度 | B. | 向左平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{12}$个单位长度 |
15.将函数y=sin($2x-\frac{π}{3})$的图象向左平移φ(φ>0)个单位后,所得到的图象对应的函数为奇函数,则φ的最小值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
12.已知0<x1<x2<x3,a=$\frac{{{{log}_2}(2{x_1}+2)}}{x_1},b=\frac{{{{log}_2}(2{x_2}+2)}}{x_2},c=\frac{{{{log}_2}(2{x_3}+2)}}{x_3}$,则a、b、c的大小关系为( )
| A. | c<a<b | B. | b<a<c | C. | a<b<c | D. | c<b<a |
13.某正三棱柱的三视图如图所示,其中正(主)视图是正方形,该正三棱柱的侧视图的面积是( )
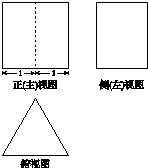

| A. | 2$\sqrt{3}$ | B. | 4 | C. | $\sqrt{3}$ | D. | 2 |