题目内容
4.设{an}是等比数列,则对任何n∈N*,都有$\frac{1}{{{a_1}{a_2}}}•\frac{1}{{{a_2}{a_3}}}…\frac{1}{{{a_n}{a_{n+1}}}}$=( )| A. | $\frac{1}{{{{({a_1}•{a_n})}^n}}}$ | B. | $\frac{1}{{{{({a_1}•{a_{n+1}})}^n}}}$ | C. | $\frac{1}{{{{({a_1}•{a_n})}^{n+1}}}}$ | D. | $\frac{1}{{{{({a_1}•{a_{n+1}})}^{n+1}}}}$ |
分析 由等比数列的性质,可得a1an+1=a2an=…=an+1a1,再由累乘法即可得到所求.
解答 解:因为a1an+1=a2an=…=an+1a1,
所以${({a_1}a_2^{\;}a_3^{\;}…{a_n}{a_{n+1}})^2}={({a_1}{a_{n+1}})^{n+1}}$,
即${a_1}a_2^2a_3^2…{a_n}^2{a_{n+1}}={({a_1}{a_{n+1}})^n}$,
故 $\frac{1}{{{a_1}{a_2}}}•\frac{1}{{{a_2}{a_3}}}…\frac{1}{{{a_n}{a_{n+1}}}}$=$\frac{1}{{{{({a_1}•{a_{n+1}})}^n}}}$.
故选B.
点评 本题主要考查等比数列的性质、累乘求积法.属于中档题.

练习册系列答案
相关题目
15.已知F为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,a为双曲线虚轴的一个顶点,过点F、A的直线与双曲线的一条渐近线在y轴右侧的交点为B,若$\overrightarrow{AB}$=($\sqrt{2}$-1)$\overrightarrow{AF}$,则此双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{5}$ |
19.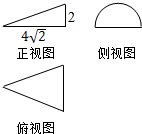 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )| A. | $\frac{8\sqrt{2}π}{3}$ | B. | $\frac{16\sqrt{2}π}{3}$ | C. | 4$\sqrt{2}π$ | D. | 8$\sqrt{2}π$ |
9.已知 F1,F2分别是双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左,右焦点,过 F1,的直线l与双曲线的左右两支分别交于点A,B,若|AB|=|AF2|,∠F1AF2=90°,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{6}+\sqrt{3}}}{2}$ | B. | $\sqrt{6}+\sqrt{3}$ | C. | $\frac{{\sqrt{5+2\sqrt{2}}}}{2}$ | D. | $\sqrt{5+2\sqrt{2}}$ |
13.某校对数学、物理两科进行学业水平考前辅导,辅导后进行测试,按成绩(满分100分)划分为合格(成绩大于或等于70分)和不合格(成绩小于70分).现随机抽取两科各100名学生的成绩统计如下:
(1)试分别估计该校学生数学、物理合格的概率;
(2)数学合格一人可以赢得4小时机器人操作时间,不合格一人则减少1小时机器人操作
时间;物理合格一人可赢得5小时机器人操作时间,不合格一人则减少2小时机器人操作时间.在(1)的前提下,
(i)记X为数学一人和物理一人所赢得的机器人操作时间(单位:小时)总和,求随机变量X 的分布列和数学期望;
(ii)随机抽取5名学生,求这5名学生物理考前辅导后进行测试所赢得的机器人操作时间不少于14小时的概率.
| 成绩(单位:分) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 数学 | 8 | 12 | 40 | 32 | 8 |
| 物理 | 7 | 18 | 40 | 29 | 6 |
(2)数学合格一人可以赢得4小时机器人操作时间,不合格一人则减少1小时机器人操作
时间;物理合格一人可赢得5小时机器人操作时间,不合格一人则减少2小时机器人操作时间.在(1)的前提下,
(i)记X为数学一人和物理一人所赢得的机器人操作时间(单位:小时)总和,求随机变量X 的分布列和数学期望;
(ii)随机抽取5名学生,求这5名学生物理考前辅导后进行测试所赢得的机器人操作时间不少于14小时的概率.
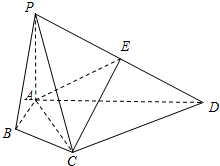 在四棱锥P-ABCD中,PA⊥平面ABCD,E是PD的中点,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,AC=AP.
在四棱锥P-ABCD中,PA⊥平面ABCD,E是PD的中点,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,AC=AP.