题目内容
5.若定义域为D的函数f(x)满足:①f(x)在D内是单调函数;
②存在[a,b]⊆D,使得f(x)在[a,b]上的值域为[$\frac{a}{2}$,$\frac{b}{2}$],则称函数f(x)为“半值函数”.
已知函h(x)=logc(cx+t)(c>0,c≠1)是“半值函数”则实数t的取值范围为( )
| A. | (0,+∞) | B. | (-∞,$\frac{1}{4}$) | C. | ($\frac{1}{4}$,+∞) | D. | (0,$\frac{1}{4}$) |
分析 根据指数函数和对数函数的图象和性质以及复合函数的单调性可知h(x)都是R上的增函数,再根据“半值函数”的定义得到logc(cx+t)=$\frac{x}{2}$,构造关于m的方程,根据根与系数的关系,即可得到结论.
解答 解:∵h(x)=logc(cx+t)(c>0,c≠1),c>1或0<c<1,h(x)都是R上的增函数,
∴$\left\{\begin{array}{l}{h(a)=\frac{a}{2}}\\{h(b)=\frac{b}{2}}\end{array}\right.$,即logc(cx+t)=$\frac{x}{2}$,即cx+t=${c}^{\frac{x}{2}}$有两不等实根,
令${c}^{\frac{x}{2}}$=m(m>0)
∴t=m-m2有两不等正根,
∴$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=1}\\{{x}_{1}•{x}_{2}=t>0}\\{△=1-4t>0}\end{array}\right.$
解得0<t<$\frac{1}{4}$.
故选:D.
点评 本题考查了新定义,以及对数函数指数函数的图象和性质,复合函数的单调性,方程根的问题,属于中档题.

练习册系列答案
相关题目
13.已知集合M={x|y=lg(1-x)},集合N={y|y=2x,x∈R},则M∩N=( )
| A. | {x|x<1} | B. | {x|x>1} | C. | {x|0<x<1} | D. | ∅ |
17.已知全集U=R,集合A={y|y=2x,x∈R},B={x|x≥2},则下图中阴影部分所表示的集合为( )
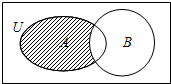

| A. | ∅ | B. | {0,1} | C. | (0,2) | D. | (-∞,2) |
 如图,点C是圆O的直径BE的延长线上一点,AC是圆O的切线,A是切点,∠ACB的平分线CD与AB相交于点D,与AE相交于点F.
如图,点C是圆O的直径BE的延长线上一点,AC是圆O的切线,A是切点,∠ACB的平分线CD与AB相交于点D,与AE相交于点F.