题目内容
6.在△ABC中,→AB−−→AB=→a+k→b,→AC=k→a+→b,其中k∈R,且|→a|=1,|→b|=2,→a与→b的夹角为120°对于以下结论:①|→a$+$→b|=√3;
②若点D是边BC的中点,则→AD=k+12(→a+→b);
③若∠A为直角,则k=5±√212;
④若∠A为钝角,则k<5−√212且k≠-1或k>5+√212;
⑤若∠A为锐角,则5−√212<k<5+√212.
其中所有正确命题的序号是①②③④⑤ (把你认为正确命题的序号都填上).
分析 由条件利用两个向量的加减法及其几何意义,两个向量的数量积的定义和公式,一元二次不等式的解法,逐一判断各个选项是否正确,从而得出结论.
解答 解:由题意可得,|→a|=1,|→b|=2,→a•→b=1×2×cos120°=-1,
∴|→a$+$→b|=√(→a+→b)2=√→a2+2→a•→b+→b2=√1−2+4=√3,故①正确.
若点D是边BC的中点,由→AB=→a+k→b,→AC=k→a+→b,可得→AD=→AB+→AC2=k+12(→a+→b),故②正确.
若∠A为直角,则→AB•→AC=(→a+k→b)•(k→a+→b )=k(→a2+→b2)+(k2+1)→a•→b=-k2+5k-1=0,求得k=5±√212,故③正确.
若∠A为钝角,则→AB•→AC=(→a+k→b)•(k→a+→b )=k(→a2+→b2)+(k2+1)→a•→b=-k2+5k-1<0,求得k<5−√212 或k>5+√212,故④正确.
若∠A为锐角,则→AB•→AC=(→a+k→b)•(k→a+→b )=k(→a2+→b2)+(k2+1)→a•→b=-k2+5k-1>0,求得5−√212k<5+√212,故⑤正确.
故答案为:①②③④⑤.
点评 本题主要考查平面向量的数量积、夹角、运算法则,一元二次不等式的解法,体现了转化的数学思想,属于中档题.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
11. 某网络广告A公司计划从甲、乙两个网站选择一个网站拓展广告业务,为此A公司随机抽取了甲、乙两个网站某月中10天的日访问量n(单位:万次),整理后得到如图茎叶图,已知A公司要从网站日访问量的平均值和稳定性两方面进行考量选择.
某网络广告A公司计划从甲、乙两个网站选择一个网站拓展广告业务,为此A公司随机抽取了甲、乙两个网站某月中10天的日访问量n(单位:万次),整理后得到如图茎叶图,已知A公司要从网站日访问量的平均值和稳定性两方面进行考量选择.
(I)请说明A公司应选择哪个网站;
(Ⅱ)现将抽取的样本分布近似看作总体分布,A公司根据所选网站的日访问量n进行付费,其付费标准如下:
求A公司每月(按30天计)应付给选定网站的费用S.
 某网络广告A公司计划从甲、乙两个网站选择一个网站拓展广告业务,为此A公司随机抽取了甲、乙两个网站某月中10天的日访问量n(单位:万次),整理后得到如图茎叶图,已知A公司要从网站日访问量的平均值和稳定性两方面进行考量选择.
某网络广告A公司计划从甲、乙两个网站选择一个网站拓展广告业务,为此A公司随机抽取了甲、乙两个网站某月中10天的日访问量n(单位:万次),整理后得到如图茎叶图,已知A公司要从网站日访问量的平均值和稳定性两方面进行考量选择.(I)请说明A公司应选择哪个网站;
(Ⅱ)现将抽取的样本分布近似看作总体分布,A公司根据所选网站的日访问量n进行付费,其付费标准如下:
| 选定网站的日访问量n(单位:万次) | A公司的付费标准(单位:元/日) |
| n<25 | 500 |
| 25≤n≤35 | 700 |
| n>35 | 1000 |
18.用辗转相除法求294和84的最大公约数,则所求最大公约数为 ( )
| A. | 21 | B. | 42 | C. | 84 | D. | 168 |
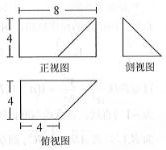 已知某几何体的三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则该几何体的体积为
已知某几何体的三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则该几何体的体积为