题目内容
7.某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示:| 积极参加班级工作 | 不积极参加班级工作 | 合计 | |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性不高 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(Ⅱ)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(Ⅲ)学生的积极性与对待班级工作的态度是否有关系?请说明理由.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (Ⅰ)随机调查这个班的一名学生,有50种情况,抽到不积极参加班级工作且学习积极性不高的学生,有19种情况,即可求出概率;
(Ⅱ)利用列举法确定基本事件的个数,即可求出两名学生中有1名男生的概率是多少?
(Ⅲ)求出K2,与临界值比较,即可得出结论.
解答 解:(Ⅰ)随机调查这个班的一名学生,有50种情况,抽到不积极参加班级工作且学习积极性不高的学生,有19种情况,故概率是${P_{\;}}=\frac{19}{50}$…(2分)
(Ⅱ)设这7名学生为a,b,c,d,e,A,B(大写为男生),则从中抽取两名学生的所有情况是:ab,ac,ad,ae,aA,aB,bc,bd,be,bA,Bb,cd,ce,cA,cB,de,dA,dB,eA,eB,AB共21种情况,其中含一名男生的有10种情况,∴${P_{\;}}=\frac{10}{21}$.…(8分)
(Ⅲ)根据${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}=\frac{{50×{{(18×19-6×7)}^2}}}{24×26×25×25}≈11.538>10.828$
∴我们有99.9%把握认为“学生的学习积极性与对待班级工作的态度”有关系.…(12分)
点评 本题考查独立性检验的应用和等可能事件的概率,本题解题的关键是正确利用观测值公式求出观测值,正确理解临界值对应的概率的意义.

练习册系列答案
相关题目
19.设命题p:?x∈R,ax2-2x+1<0,则命题p为假命题的一个充分不必要条件是( )
| A. | a≥1 | B. | a>1 | C. | a≤1 | D. | a<2 |
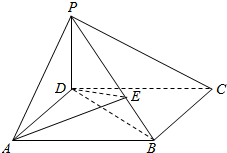 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为平行四边形,∠ADB=90°,AB=2AD.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为平行四边形,∠ADB=90°,AB=2AD.