题目内容
2.已知函数f(x)=sinx,x∈(1,3),则使得f′(x)>0的概率为$\frac{π-2}{4}$.分析 求函数的导数,利用几何概型的概率公式进行求解即可.
解答 解:函数的f(x)的导数f′(x)=cosx,
由f′(x)>0得cosx>0,
解得1<x<$\frac{π}{2}$,
则f′(x)>0的概率P=$\frac{\frac{π}{2}-1}{3-1}$=$\frac{π-2}{4}$,
故答案为:$\frac{π-2}{4}$
点评 本题主要考查几何概型的概率的计算,根据导数公式求出不等式的等价条件是解决本题的关键.

练习册系列答案
相关题目
12. 将正整数按如图排列,其中处于从左到右第m列从下到上第n行的数
将正整数按如图排列,其中处于从左到右第m列从下到上第n行的数
记为A(m,n),如A(3,1)=4,A(4,2)=12,则A(10,3)
=69;A(1,n)=$\frac{n(n+1)}{2}$.
 将正整数按如图排列,其中处于从左到右第m列从下到上第n行的数
将正整数按如图排列,其中处于从左到右第m列从下到上第n行的数记为A(m,n),如A(3,1)=4,A(4,2)=12,则A(10,3)
=69;A(1,n)=$\frac{n(n+1)}{2}$.
17.若变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≤8}\\{2y-x≤4}\\{x≥0}\\{y≥0}\end{array}\right.$,且z=4y-x的最大值为a,最小值为b,则a+b的值是( )
| A. | 10 | B. | 20 | C. | 4 | D. | 12 |
7.某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示:
(Ⅰ)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(Ⅱ)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(Ⅲ)学生的积极性与对待班级工作的态度是否有关系?请说明理由.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 积极参加班级工作 | 不积极参加班级工作 | 合计 | |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性不高 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(Ⅱ)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(Ⅲ)学生的积极性与对待班级工作的态度是否有关系?请说明理由.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
11.某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金不超过54万元,假设种植黄瓜和韭菜的产量、成本和售价如表:
为使一年的种植总利润(总利润=总销售收入-总种植成本)最大,那么黄瓜和韭菜的种植面积(单位:亩)分别为30;20.
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 6吨 | 0.9万元 | 0.3万元 |
12.设变量x、y满足线性约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}\right.$则目标函数z=log2(2x+y)的最大值为( )
| A. | log2$\frac{3}{2}$ | B. | log23 | C. | 1 | D. | 不存在 |
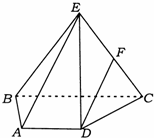 已知四棱锥E-A BCD中,AD∥BC,AD=$\frac{1}{2}$BC=1,△BCE为等边三角形,且面BCE⊥面ABCD,点F为CE中点.
已知四棱锥E-A BCD中,AD∥BC,AD=$\frac{1}{2}$BC=1,△BCE为等边三角形,且面BCE⊥面ABCD,点F为CE中点.