例1(课本第82页
例2)用计算机作出的图像,并在同一坐标系下作出下列函数的图象,并指出它们与指数函数y=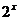 的图象的关系,
的图象的关系,
⑴y=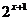 与y=
与y=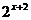 .
⑵y=
.
⑵y=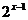 与y=
与y=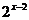 .
.
解:⑴作出图像,显示出函数数据表
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
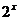 |
0.125 |
0.25 |
0.5 |
1 |
2 |
4 |
8 |
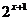 |
0.25 |
0.5 |
1 |
2 |
4 |
8 |
16 |
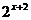 |
0.5 |
1 |
2 |
4 |
8 |
16 |
32 |
 比较函数y=
比较函数y=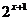 、y=
、y=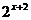 与y=
与y=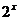 的关系:将指数函数y=
的关系:将指数函数y=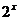 的图象向左平行移动1个单位长度,就得到函数y=
的图象向左平行移动1个单位长度,就得到函数y=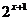 的图象,将指数函数y=
的图象,将指数函数y=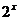 的图象向左平行移动2个单位长度,就得到函数y=
的图象向左平行移动2个单位长度,就得到函数y=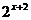 的图象
的图象
⑵作出图像,显示出函数数据表
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
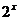 |
0.125 |
0.25 |
0.5 |
1 |
2 |
4 |
8 |
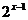 |
0.625 |
0.125 |
0.25 |
0.5 |
1 |
2 |
4 |
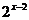 |
0.3125 |
0.625 |
0.125 |
0.25 |
0.5 |
1 |
2 |
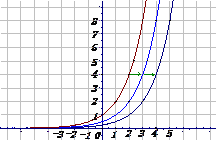 比较函数y=
比较函数y=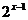 、y=
、y=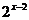 与y=
与y=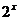 的关系:将指数函数y=
的关系:将指数函数y=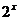 的图象向右平行移动1个单位长度,就得到函数y=
的图象向右平行移动1个单位长度,就得到函数y=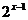 的图象,将指数函数y=
的图象,将指数函数y=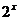 的图象向右平行移动2个单位长度,就得到函数y=
的图象向右平行移动2个单位长度,就得到函数y=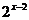 的图象
的图象
小结:⑴
y=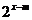 与y=
与y=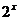 的关系:当m>0时,将指数函数y=
的关系:当m>0时,将指数函数y=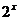 的图象向右平行移动m个单位长度,就得到函数y=
的图象向右平行移动m个单位长度,就得到函数y=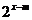 的图象;当m<0时,将指数函数y=
的图象;当m<0时,将指数函数y=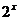 的图象向左平行移动m个单位长度,就得到函数y=
的图象向左平行移动m个单位长度,就得到函数y=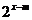 的图象
的图象
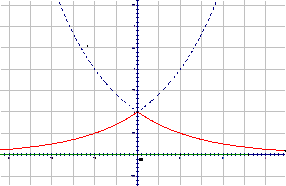 例2 ⑴已知函数
例2 ⑴已知函数
 用计算器或计算机作出函数图像,求定义域、值域,并探讨
用计算器或计算机作出函数图像,求定义域、值域,并探讨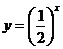 与
与 图像的关系
图像的关系
解: 定义域:xÎR 值域:
定义域:xÎR 值域: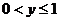
关系:将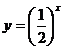 的图像y轴右侧的部分翻折到y轴左侧的到
的图像y轴右侧的部分翻折到y轴左侧的到 的图像,关于y轴对称.
的图像,关于y轴对称.
 ⑵已知函数
⑵已知函数
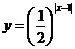 用计算器或计算机作出函数图像,求定义域、值域,并探讨
用计算器或计算机作出函数图像,求定义域、值域,并探讨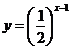 与
与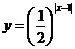 图像的关系
图像的关系
解: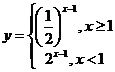 定义域:xÎR 值域:
定义域:xÎR 值域: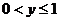
关系:将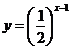 (x>1)的图像在直线x=1右侧的部分翻折到直线x=1左侧得到
(x>1)的图像在直线x=1右侧的部分翻折到直线x=1左侧得到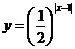 的图像,是关于直线x=1对称
的图像,是关于直线x=1对称
⑵推广:对于有些复合函数的图象,则常用基本函数图象+变换方法作出:
基本函数图象+变换:即把我们熟知的基本函数图象,通过平移、作其对称图等方法,得到我们所要求作的复合函数的图象,如上例,这种方法我们遇到的有以下几种形式:
|
函
数 |
y=f(x) |
|
y=f(x+a) |
a>0时,向左平移a个单位;a<0时,向右平移|a|个单位. |
|
y=f(x)+a |
a>0时,向上平移a个单位;a<0时,向下平移|a|个单位. |
|
y=f(-x) |
y=f(-x)与y=f(x)的图象关于y轴对称. |
|
y=-f(x) |
y=-f(x)与y=f(x)的图象关于x轴对称. |
|
y=-f(-x) |
y=-f(-x)与y=f(x)的图象关于原点轴对称. |
|
y=f(|x|) |
y=f(|x|)的图象关于y轴对称,x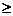 0时函数即y=f(x),所以x<0时的图象与x 0时函数即y=f(x),所以x<0时的图象与x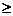 0时y=f(x)的图象关于y轴对称. 0时y=f(x)的图象关于y轴对称. |
|
y=|f(x)| |
∵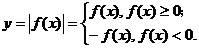 ,∴y=|f(x)|的图象是y=f(x) ,∴y=|f(x)|的图象是y=f(x)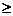 0与y=f(x)<0图象的组合. 0与y=f(x)<0图象的组合. |
y= |
y= 与y=f(x)的图象关于直线y=x对称. 与y=f(x)的图象关于直线y=x对称. |
以上是在高一阶段我们看到的几种函数图象的变换,但随着知识的增加,还会有许多较复杂的变换,以后再作研究.
例3探讨函数 和
和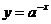
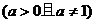 的图象的关系,并证明关
的图象的关系,并证明关
于y轴对称
证:设P( ,
,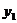 )是函数
)是函数
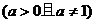 的图象上任意一点
的图象上任意一点
则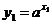 而P(
而P( ,
,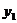 )关于y轴的对称点Q是(-
)关于y轴的对称点Q是(- ,
,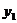 )
)
∴ 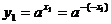 即Q在函数
即Q在函数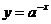 的图象上
的图象上
由于P是任意取的,所以 上任一点关于y轴的对称点都在
上任一点关于y轴的对称点都在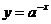 的图象上
的图象上
同理可证: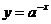 图象上任意一点也一定在函数
图象上任意一点也一定在函数 的图象上
的图象上
∴ 函数 和
和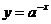 的图象关于y轴对称
的图象关于y轴对称
 例4 已知函数
例4 已知函数 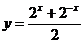 求函数的定义域、值域
求函数的定义域、值域
解:作出函数图像,观察分析讨论,教师引导、整理
定义域为
R
由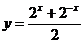 得
得 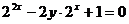
∵xÎR, ∴△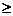 0, 即
0, 即  , ∴
, ∴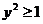 , 又∵
, 又∵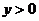 ,∴
,∴
 存在反函数,且对于任意x
存在反函数,且对于任意x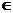 R恒有
R恒有 =2,则
=2,则 的值是
的值是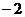 B.0
C.2
D.不确定,与x有关
B.0
C.2
D.不确定,与x有关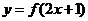 是奇函数,则函数
是奇函数,则函数 的图象.
的图象.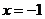 B.有对称轴
B.有对称轴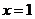 C.有对称点
C.有对称点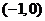 D.有对称点
D.有对称点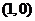
 上的偶函数
上的偶函数 ,且在
,且在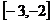 上是减函数,
上是减函数,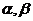 是锐角三角形的两个内角,则( )
是锐角三角形的两个内角,则( )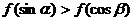 B.
B. 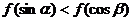
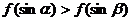 D.
D.
 ,则
,则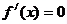 有 .
有 .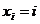 (
(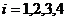 )
B.分别位于区间(1,2) (2,3) (3,4)内三个根
)
B.分别位于区间(1,2) (2,3) (3,4)内三个根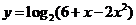 的一个单调递减区间是.
的一个单调递减区间是. B.
B.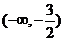 C.
C. D.
D.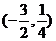
 ≤4,条件
≤4,条件 ≤
≤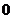 ,则
,则 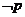 是
是 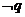 的
的 ,
,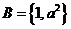 ,若
,若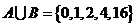 ,则
,则 的值为
的值为 , 向量
, 向量 , 且
, 且 , 动点
, 动点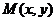 的轨迹为E.
的轨迹为E.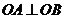 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;