1.(2009安徽卷理)若不等式组 所表示的平面区域被直线
所表示的平面区域被直线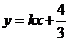 分为面积相等的两部分,则
分为面积相等的两部分,则 的值是
的值是
 (A)
(A)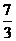 (B)
(B) 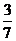 (C)
(C)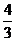 (D)
(D) 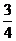
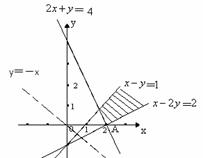
 [解析]:不等式表示的平面区域如图所示阴影部分△ABC
[解析]:不等式表示的平面区域如图所示阴影部分△ABC
由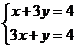 得A(1,1),又B(0,4),C(0,
得A(1,1),又B(0,4),C(0,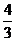 )
)
∴ △ABC=
△ABC=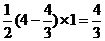 ,设
,设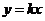 与
与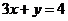 的
的
交点为D,则由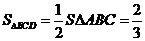 知
知 ,∴
,∴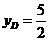
∴ 选A。
选A。
2(2009安徽卷文)不等式组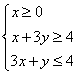 所表示的平面区域的面积等于
所表示的平面区域的面积等于
A. 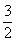 B.
B. 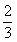
C. 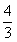 D.
D. 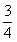
[解析]由 可得
可得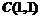 ,故
,故 阴 =
阴 = ,选C。
,选C。
[答案]C
3(2009安徽卷文)“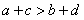 ”是“
”是“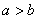 且
且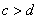 ”的
”的
A. 必要不充分条件 B. 充分不必要条件
C. 充分必要条件 D. 既不充分也不必要条件
[解析]易得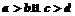 时必有
时必有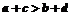 .若
.若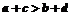 时,则可能有
时,则可能有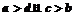 ,选A。
,选A。
[答案]A
4(2009四川卷文)已知 ,
,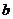 ,
,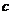 ,
,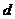 为实数,且
为实数,且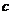 >
>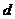 .则“
.则“ >
>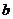 ”是“
”是“ -
-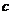 >
>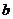 -
-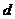 ”的
”的
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
[答案]B 

[解析]显然,充分性不成立.又,若 -
-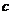 >
>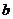 -
-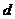 和
和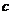 >
>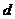 都成立,则同向不等式相加得
都成立,则同向不等式相加得 >
>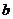
即由“ -
-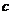 >
>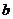 -
-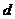 ”
”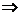 “
“ >
>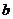 ”
”
5(2009四川卷文)某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元。该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.那么该企业可获得最大利润是
A. 12万元 B. 20万元 C. 25万元 D. 27万元
[答案]D
 [解析]设生产甲产品
[解析]设生产甲产品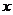 吨,生产乙产品
吨,生产乙产品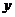 吨,则有关系:
吨,则有关系:
|
|
A原料 |
B原料 |
甲产品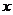 吨 吨 |
3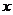 |
2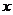 |
乙产品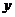 吨 吨 |
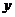 |
3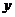 |
则有: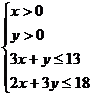
目标函数
作出可行域后求出可行域边界上各端点的坐标,经验证知:
当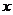 =3,
=3,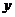 =5时可获得最大利润为27万元,故选D
=5时可获得最大利润为27万元,故选D
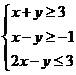 .则目标函数z=2x+3y的最小值为
.则目标函数z=2x+3y的最小值为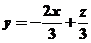 在可行域上平移,知在点B自目标函数取到最小值,解方程组
在可行域上平移,知在点B自目标函数取到最小值,解方程组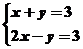 得
得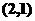 ,所以
,所以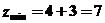 ,故选择B。
,故选择B。 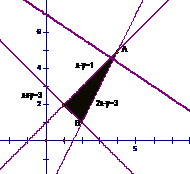
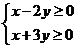 ,所确定的平面区域,则圆
,所确定的平面区域,则圆 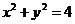 在区域D内
在区域D内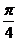 B
B C
C  D
D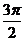


 ,所以圆心角
,所以圆心角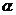 即为两直线的所成夹角,所以
即为两直线的所成夹角,所以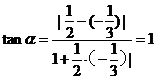 ,所以
,所以 ,而圆的半径是2,所以弧长是
,而圆的半径是2,所以弧长是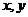 满足
满足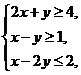 则
则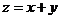

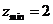 ,但无最大值。选B.
,但无最大值。选B.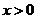 ,则
,则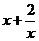 的最小值为
的最小值为  .
.
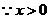
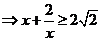 ,当且仅当
,当且仅当 时取等号.
时取等号.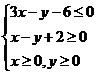 ,
, 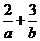 的最小值为( ).
的最小值为( ). 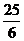 B.
B. C.
C. 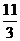 D.
4
D.
4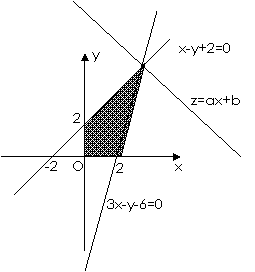
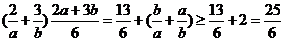 ,故选A.
,故选A.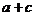 >b+d
, q:
>b+d
, q: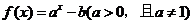 的图像不过第二象限
的图像不过第二象限 
 在
在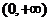 上为增函数
上为增函数 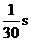 。问该中子星的最小密度应是多少才能维持该星体的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。
。问该中子星的最小密度应是多少才能维持该星体的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。