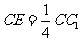(1)已知两角和一边(如: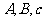 ) 解法:
) 解法: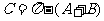 ;
;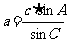 ;
;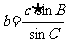 .
.
(2)已知两边和夹角(如: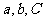 )
)
解法: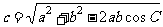 ;由
;由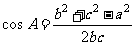 求
求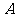 ;
;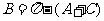 .
.
(3)已知三边(如: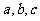 )
)
解法:由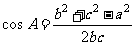 求
求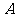 ;由
;由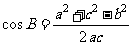 求
求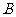 ;
;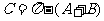 .
.
(4)已知两边和其中一边对角(如: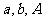 )(注意讨论解的情况)
)(注意讨论解的情况)
解法1: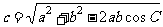 ;由余弦定理推论求
;由余弦定理推论求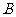 ;
;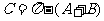 .
.
解法2:由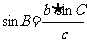 求
求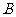 ;
;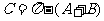 ;
;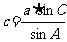 .
.
如1)在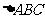 中,A>B是
中,A>B是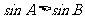 成立的_____条件(答:充要);
成立的_____条件(答:充要);
2)在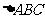 中,
中, 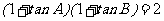 ,则
,则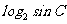 =_____(答:
=_____(答: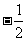 );
);
3)在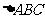 中,
中,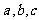 分别是角A、B、C所对的边,若
分别是角A、B、C所对的边,若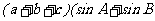
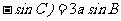 ,则
,则 =
=
(答: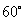 );
);
4)在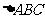 中,若其面积
中,若其面积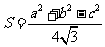 ,则
,则 =____
(答:
=____
(答: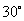 );
);
5)在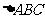 中,
中,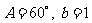 ,这个三角形的面积为
,这个三角形的面积为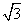 ,则
,则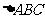 外接圆的直径是____(答:
外接圆的直径是____(答: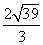 );
);
6)在△ABC中,a、b、c是角A、B、C的对边,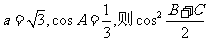 = ,
= ,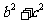 的最大值为
的最大值为
(答: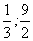 );
);
7)在△ABC中AB=1,BC=2,则角C的取值范围是 (答: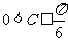 );
);
8)设O是锐角三角形ABC的外心,若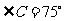 ,且
,且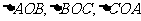 的面积满足关系式
的面积满足关系式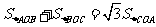 ,求
,求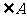 (答:
(答: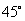 ).
).
9)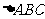 中,若
中,若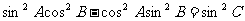 ,判断
,判断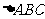 的形状(答:直角三角形)。
的形状(答:直角三角形)。
10)在锐角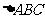 中,
中,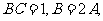 则
则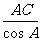 的值等于 2 ,
的值等于 2 ,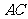 的取值范围为
的取值范围为 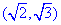 .
.
11)已知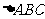 中,
中,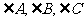 的对边分别为
的对边分别为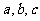 若
若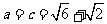 且
且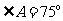 ,则
,则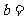 (答:2);
(答:2);
12)在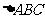 中,内角A、B、C的对边长分别为
中,内角A、B、C的对边长分别为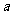 、
、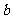 、
、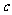 ,已知
,已知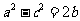 ,且
,且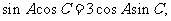 求b
求b 
 (答:4);
(答:4);
13)在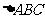 中,角
中,角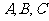 所对的边分别为
所对的边分别为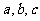 ,且满足
,且满足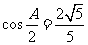 ,
,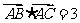 .
.
(I)求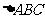 的面积; (II)若
的面积; (II)若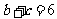 ,求
,求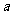 的值.
(答:2;
的值.
(答:2; 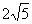 );
);
21、 在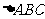 中,已知
中,已知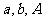 ,则
,则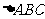 解的情况为:
解的情况为:
|
|
  为锐角 为锐角 |
 为钝角或直角 为钝角或直角 |
||
|
图 形 |
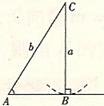 |
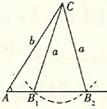 |
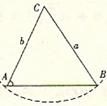 |
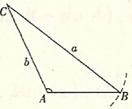 |
|
关系式 |
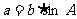 |
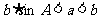 |
 |
 |
|
解的 个数 |
一解 |
两解 |
一解 |
一解 |
(注:上表中,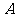 为锐角时,若
为锐角时,若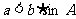 ,无解;
,无解;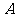 为钝角或直角时,若
为钝角或直角时,若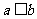 ,无解.)
,无解.)
如 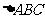 中,A、B的对边分别是
中,A、B的对边分别是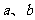 ,且
,且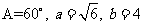 ,那么满足条件的
,那么满足条件的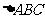
A、 有一个解 B、有两个解 C、无解 D、不能确定 (答:C);
 ,这是三角形中三角函数问题的特殊性,解题可不能忘记!任意两角和与第三个角总互补,任意两半角和与第三个角的半角总互余.锐角三角形
,这是三角形中三角函数问题的特殊性,解题可不能忘记!任意两角和与第三个角总互补,任意两半角和与第三个角的半角总互余.锐角三角形 三内角都是锐角
三内角都是锐角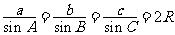 (R为三角形外接圆的半径).注意:
(R为三角形外接圆的半径).注意: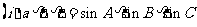 ;
;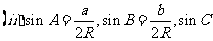
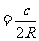 ;
;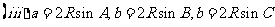 ;
;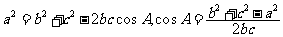 等,常用余弦定理鉴定三角形形状.
等,常用余弦定理鉴定三角形形状.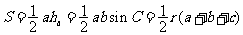 等等(其中
等等(其中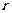 为三角形内切圆半径).
为三角形内切圆半径).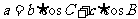 ;
;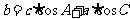 ;
; 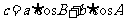 .
.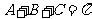 这个特殊性:
这个特殊性: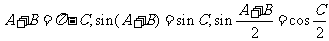 ;
;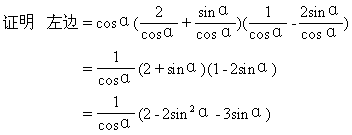
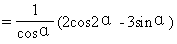

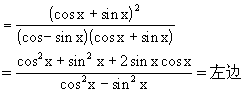
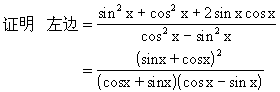
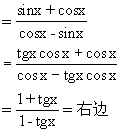
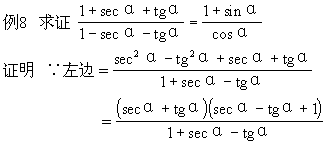
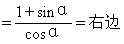
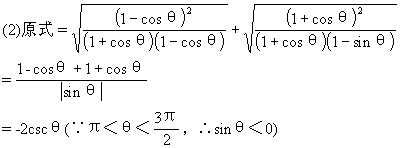
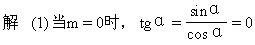
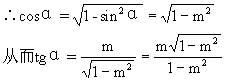
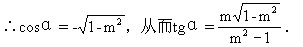
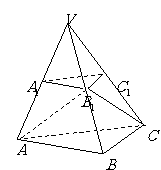
 平行于三棱锥
平行于三棱锥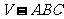 的底面,等边三角形
的底面,等边三角形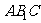 所在平面与面
所在平面与面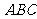 垂直,且
垂直,且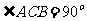 ,设
,设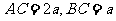 。
。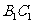 为异面直线
为异面直线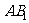 与
与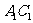 的公垂线;
的公垂线;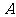 与平面
与平面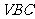 的距离;
的距离;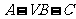 的大小。
的大小。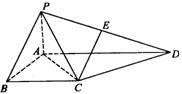 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB,底面ABCD为直角梯形,
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB,底面ABCD为直角梯形,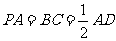 .
.