摘要:2.三角函数式的化简 三角函数式的化简的结果应满足下述要求: (1)函数种类尽可能地少. (2)次数尽可能地低. (3)项数尽可能地少. (4)尽可能地不含分母. (5)尽可能地将根号中的因式移到根号外面来. 化简的总思路是:尽可能地化为同类函数再化简. 例3 化简sin2α·tgα+cos2α·ctgα+2sinαcosα =secα·cscα 解2 原式=(sin2α·tgα+sinα·cosα)+(cos2α·ctgα+sinαcosα) =tgα·(sin2α+cos2α)+ctgα(sin2α+cos2α) =tgα+ctgα =secα·cscα 说明 (1)在解1中.将正切.余切化为正弦.余弦再化简.仍然是循着减少函数种类的思路进行的. (2)解2中的逆用公式将sinα·cosα用tgα表示.较为灵活.解1与解2相比.思路更自然.因而更实用. 例4 化简: 分析 将被开方式配成完全平方式.脱去根号.进行化简.
网址:http://m.1010jiajiao.com/timu_id_4009857[举报]
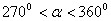 ,三角函数式
,三角函数式 的化简结果为( )
的化简结果为( )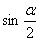 B.
B.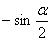 C.
C.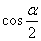 D.
D.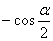
 ,三角函数式
,三角函数式 的化简结果为( )
的化简结果为( )



 ,三角函数式
,三角函数式 的化简结果为( )
的化简结果为( )



 化成三角函数的积的形式(要求结果最简).
化成三角函数的积的形式(要求结果最简). 化成三角函数的积的形式(要求结果最简).
化成三角函数的积的形式(要求结果最简).