19.用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图所示的花圃,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.
(1)求恰有两个区域用红色鲜花的概率;
(2)记花圃中红色鲜花区域的块数为X,求X的分布列及其数学期望.
解:(1)设M表示事件“恰有两个区域用红色鲜花”,如图,当区域A、D同色时,共有5×4×3×1×3=180种;
当区域A、D不同色时,共有5×4×3×2×2=240种;
|
A |
||
|
B |
C |
E |
|
D |
因此,所有基本事件总数为:180+240=420种.
它们是等可能的.
又因为A、D为红色时,共有4×3×3=36种;
B、E为红色时,共有4×3×3=36种;
因此,事件M包含的基本事件有:36+36=72种.
所以,恰有两个区域用红色鲜花的概率P(M)==.
(2)随机变量X的取值分别为0,1,2.
则当X=0时,用黄、蓝、白、橙四种颜色来涂色,
若A、D为同色时,共有4×3×2×1×2=48种;
若A、D为不同色时,共有4×3×2×1×1=24种;
即X=0所包含的基本事件有48+24=72种,
所以P(X=0)==;
由第(1)问得P(X=2)=;
所以P(X=1)=1--=.
从而随机变量X的分布列为:
|
X |
0 |
1 |
2 |
|
P |
|
|
|
所以,E(X)=0×+1×+2×=1.
12.在平面直角坐标系xOy中,设D是横坐标与纵坐标的绝对值均不大于2的点构成的区域,E是到原点的距离不大于1的点构成的区域,向D中随机投一点,则所投的点落在E中的概率是__________.
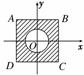 解析:如图:区域D表示边长为4的正方形ABCD的内部(含边界),区域E表示单位圆及其内部,因此P=
解析:如图:区域D表示边长为4的正方形ABCD的内部(含边界),区域E表示单位圆及其内部,因此P=
答案:
13(2009·广东高考)已知离散型随机变量X的分布列如下表.若E(X)=0,D(X)=1,则a=________,b=________.
|
X |
-1 |
0 |
1 |
2 |
|
P |
a |
b |
c |
|
解析:由题意
解得a=,b=c=.
答案:
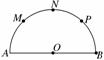 如图,已知AB是半圆O的直径,AB=8,M、N、
P是将半圆圆周
如图,已知AB是半圆O的直径,AB=8,M、N、
P是将半圆圆周 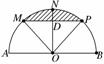 所以这3个点组成直角三角形的概率P=.
所以这3个点组成直角三角形的概率P=. ×2
×2 ×8=8
×8=8 ×42-
×42-
 (sinx+cosx)dx则二项式(a-)6展开式中含x2的项的系数是________.
(sinx+cosx)dx则二项式(a-)6展开式中含x2的项的系数是________.

 (-)r
(-)r =C
=C  .
.