摘要：17．如图.已知AB是半圆O的直径.AB＝8.M.N. P是将半圆圆周 四等分的三个分点． (1)从A.B.M.N.P这5个点中任取3个点.求这3个点组成直角 三角形的概率, (2)在半圆内任取一点S.求三角形SAB的面积大于8的概率． 解:(1)从A.B.M.N.P这5个点中任取3个点.一共可以组成10个三角形:ABM.ABN.ABP.AMN.AMP.ANP.BMN.BMP.BNP.MNP.其中是直角三角形的只有ABM.ABN.ABP 3个. 所以这3个点组成直角三角形的概率P＝. (2)连结MP.取线段MP的中点D.则OD⊥MP. 易求得OD＝2. 当S点在线段MP上时.S△ABS=×2×8=8. 所以只有当S点落在阴影部分时.三角形SAB面积才能大于8.而 S阴影=S扇形OMP-S△OMP=××42-×42=4π-8. 所以由几何概型公式得三角形SAB的面积大于8的概率P=
网址：http://m.1010jiajiao.com/timu_id_3971558[举报]
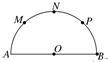如图，已知AB是半圆O的直径，AB=8，M、N、P是将半圆圆周四等分的三个分点（1）从A、B、M、N、P这5个点中任取3个点，求这3个点组成直角三角形的概率；
（2）在半圆内任取一点S，求三角形SAB的面积大于8
| 2 |
如图，已知AB是半圆O的直径，AB=8，M、N、P是将半圆圆周四等分的三个分点
（1）从A、B、M、N、P这5个点中任取3个点，求这3个点组成直角三角形的概率；
（2）在半圆内任取一点S，求三角形SAB的面积大于8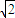
的概率．
查看习题详情和答案>>
（1）从A、B、M、N、P这5个点中任取3个点，求这3个点组成直角三角形的概率；
（2）在半圆内任取一点S，求三角形SAB的面积大于8
的概率．
查看习题详情和答案>>
等于
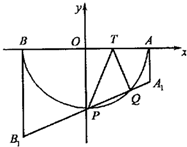已知T是半圆O的直径AB上一点，AB=2，OT=t（0＜t＜1）．以AB为腰的直角梯形AA1B1B中，AA1垂直于AT，且|AA1|=|AT|，BB1垂直于BT，且|BB1|=|BT|，A1B1交半圆于P，Q两点，建立如图所示直角坐标系，O为坐标原点．
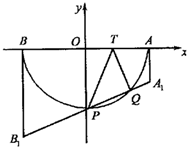已知T是半圆O的直径AB上一点，AB=2，OT=t（0＜t＜1）．以AB为腰的直角梯形AA1B1B中，AA1垂直于AT，且|AA1|=|AT|，BB1垂直于BT，且|BB1|=|BT|，A1B1交半圆于P，Q两点，建立如图所示直角坐标系，O为坐标原点．