4、已知函数 满足
满足 (其中
(其中 为
为 在点
在点 处的导数,
处的导数, 为常数).
为常数).
(1)求函数 的单调区间;
的单调区间;
(2)若方程 有且只有两个不等的实数根,求常数
有且只有两个不等的实数根,求常数 ;
;
(3)在(2)的条件下,若 ,求函数
,求函数 的图象与
的图象与 轴围成的封闭图形的面积.
轴围成的封闭图形的面积.
解:(1)由 ,得
,得 .
.
取 ,得
,得 ,解之,得
,解之,得 ,
,
∴ . ……………………………………2分
. ……………………………………2分
从而 ,
,
列表如下:
 |
 |
 |
 |
1 |
 |
 |
+ |
0 |
- |
0 |
+ |
 |
↗ |
有极大值 |
↘ |
有极小值 |
↗ |
∴ 的单调递增区间是
的单调递增区间是 和
和 ;
; 的单调递减区间是
的单调递减区间是 .………………4分
.………………4分
(2)由(1)知, ;
;
 .………………………………6分
.………………………………6分
∴方程 有且只有两个不等的实数根,等价于
有且只有两个不等的实数根,等价于 或
或 .
………8分
.
………8分
∴常数 或
或 .
……………………………………9分
.
……………………………………9分
(3)由(2)知, 或
或 .
.
而 ,所以
,所以 .………………10分
.………………10分
令 ,得
,得 ,
, ,
, .……………………………12分
.……………………………12分
∴所求封闭图形的面积

 .………………14分
.………………14分
 ,则满足条件
,则满足条件 的点
的点 所在区域的面积为( B )
所在区域的面积为( B ) B.
B. C.
C. D.
D.


 为定义域上的单调函数,求实数
为定义域上的单调函数,求实数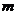 的取值范围;
的取值范围; 时,求函数
时,求函数 时,且
时,且 ,证明:
,证明: .
. ∴
∴
 ,有
,有
 ,对
,对 恒成立,∴
恒成立,∴ ,而
,而 ,所以
,所以
 对
对 ,得
,得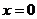
 时,
时,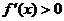 ,当
,当 时,
时,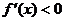
 ………7分
………7分 对
对 ,∵
,∵

 ∴
∴
 同理可得
同理可得

 ∴
∴ 上递增
上递增
 在
在 上总有
上总有 ,即
,即 在
在 时,
时, ,即
,即

 由(2)它在
由(2)它在
 ,
, ∵
∵ ,综上
,综上
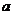 、使得关于
、使得关于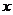 的不等式
的不等式 在(0,
在(0, )上恒成立,若存在,求出
)上恒成立,若存在,求出 (其中
(其中 为自然对数的底数).
为自然对数的底数). 上恒成立,
上恒成立, 在
在 ,则
,则 ,
∴
,
∴ ,
,
 ,则
,则 时,
时, 恒成立,
恒成立, 上为减函数
上为减函数 在
在 显然不满足条件,
显然不满足条件, ,则
,则 时,
时, ,
∴
,
∴ 时
时 ,
, 上为增函数,当
上为增函数,当 ,不能使
,不能使 在
在 ,
即
,
即 ,
, ,即可证得
,即可证得 对一切正整数
对一切正整数 成立.
成立.  ;②
;② ,其中是“科比函数”的函数序号是
② .
,其中是“科比函数”的函数序号是
② . 是“科比函数”,则实数k的取值范围是
是“科比函数”,则实数k的取值范围是 .
.