8. 东城一模(文). 已知函数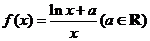 .
.
(Ⅰ)若曲线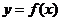 在点
在点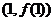 处的切线与直线
处的切线与直线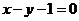 平行,求
平行,求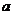 的值;
的值;
(Ⅱ)求函数 的单调区间和极值;
的单调区间和极值;
(Ⅲ)当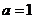 ,且
,且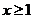 时,证明:
时,证明: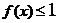 .
.
(Ⅰ)解:函数 的定义域为
的定义域为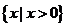 ,
,
所以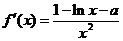 .
.
又曲线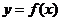 在点
在点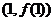 处的切线与直线
处的切线与直线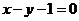 平行,
平行,
所以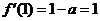 ,即
,即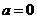 .……………………………………4分
.……………………………………4分
(Ⅱ)令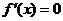 ,得
,得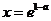 .
.
当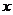 变化时,
变化时,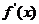 ,
, 的变化情况如下表:
的变化情况如下表:
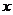 |
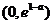 |
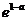 |
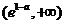 |
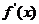 |
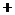 |
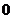 |
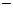 |
 |
 |
极大值 |
 |
由表可知: 的单调递增区间是
的单调递增区间是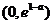 ,单调递减区间是
,单调递减区间是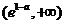 .
.
所以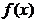 在
在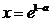 处取得极大值,
处取得极大值,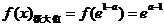 .………………9分
.………………9分
(Ⅲ)当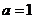 时,
时,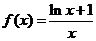 .
.
由于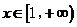 ,要证
,要证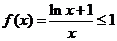 ,
,
故只需证明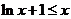 .
.
令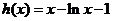 ,
则
,
则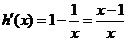 .
.
因为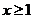 ,所以
,所以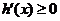 ,故
,故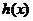 在
在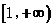 上单调递增,
上单调递增,
当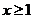 时,
时,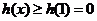 ,即
,即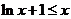 成立.
成立.
故当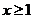 时,有
时,有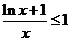 .即
.即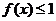 .……………………………………13分
.……………………………………13分
9 西城一模(文)已知函数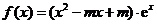 (
(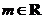 ).
).
(Ⅰ)若函数 存在零点,求实数
存在零点,求实数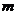 的取值范围;
的取值范围;
(Ⅱ)当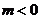 时,求函数
时,求函数 的单调区间;并确定此时
的单调区间;并确定此时 是否存在最小值,如果存在,求出最小值,如果不存在,请说明理由.
是否存在最小值,如果存在,求出最小值,如果不存在,请说明理由.
解:(Ⅰ)设 有零点,即函数
有零点,即函数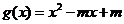 有零点,
有零点,
所以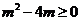 ,解得
,解得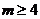 或
或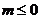 .…………………3分
.…………………3分
(Ⅱ)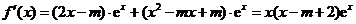 , …………………5分
, …………………5分
令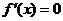 ,得
,得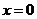 或
或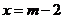 ,
,
因为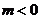 时,所以
时,所以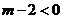 ,
,
当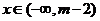 时,
时,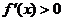 ,函数
,函数 单调递增;
单调递增;
当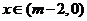 时,
时,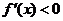 ,函数
,函数 单调递减;
单调递减;
当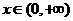 时,
时,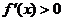 ,函数
,函数 单调递增.
…………………7分
单调递增.
…………………7分
此时, 存在最小值.
…………………8分
存在最小值.
…………………8分
 的极小值为
的极小值为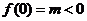 .
…………………9分
.
…………………9分
根据 的单调性,
的单调性, 在区间
在区间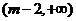 上的最小值为
上的最小值为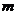 , …………10分
, …………10分
解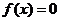 ,得
,得 的零点为
的零点为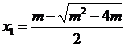 和
和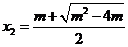 ,
,
结合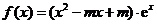 ,
,
可得在区间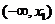 和
和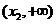 上,
上,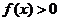 .
…………………11分
.
…………………11分
因为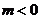 ,所以
,所以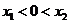 ,
,
并且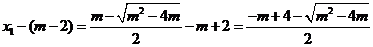
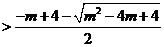
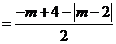
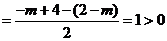 ,
,
即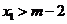 ,
…………………13分
,
…………………13分
综上,在区间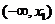 和
和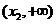 上,
上,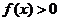 ,
, 在区间
在区间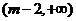 上的最小值为
上的最小值为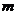 ,
,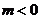 ,
,
所以,当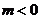 时
时 存在最小值,最小值为
存在最小值,最小值为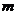 .
…………………14分
.
…………………14分
10怀柔一模(文)14.已知函数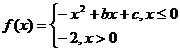 ,若
,若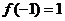 ,
,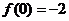 ,则函数
,则函数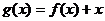 的零点个数为
____.3
的零点个数为
____.3
11东城二模(文)7. 若函数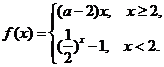 是
是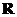 上的单调减函数,则实数
上的单调减函数,则实数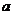 的取值范围是( B )
的取值范围是( B )
A.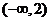 B.
B.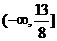 C.
C.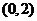 D.
D.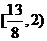
6、已知函数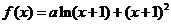 在
在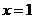 处有极值.
处有极值.
(Ⅰ)求实数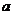 值;
值;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)试问是否存在实数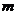 ,使得不等式
,使得不等式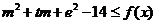 对任意
对任意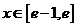 及
及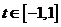
恒成立?若存在,求出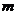 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.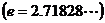
解:(Ⅰ)因为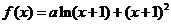 ,
,
所以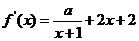 .
……2分
.
……2分
由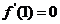 ,可得
,可得
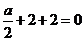 ,
,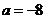 .
.
经检验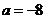 时,函数
时,函数 在
在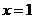 处取得极值,
处取得极值,
所以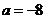 .
………4分
.
………4分
(Ⅱ)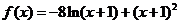 ,
,
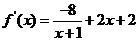
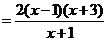 .
……6分
.
……6分
而函数 的定义域为
的定义域为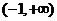 ,
,
当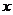 变化时,
变化时,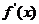 ,
, 的变化情况如下表:
的变化情况如下表:
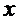 |
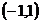 |
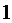 |
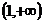 |
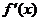 |
- |
0 |
+ |
 |
↘ |
极小值 |
↗ |
由表可知, 的单调减区间为
的单调减区间为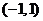 ,
, 的单调减区间为
的单调减区间为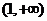 .……9分
.……9分
(3)∵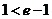 ,
,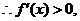
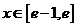 时,
时,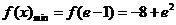 …10分
…10分
不等式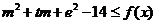 对任意
对任意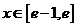 及
及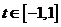 恒成立,即
恒成立,即
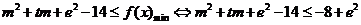 ,
,
即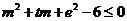 对
对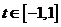 恒成立,
…12分
恒成立,
…12分
令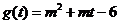 ,
,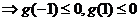
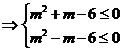 ,
,
解得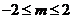 为所求.
…14分
为所求.
…14分
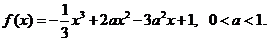
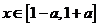 时,恒有
时,恒有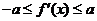 成立(其中
成立(其中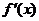 是函数
是函数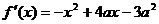 ,且
,且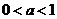 , …………………………………1分
, …………………………………1分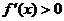 时,得
时,得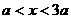 ;
;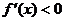 时,得
时,得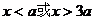 ;
;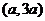 ;
;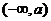 和
和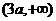 .
………………………………5分
.
………………………………5分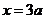 时,
时,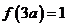 . ………………6分
. ………………6分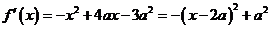 ,
,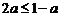 时,即
时,即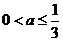 时,
时, 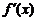 在区间
在区间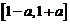 内单调递减.
内单调递减. 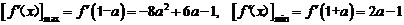 .
.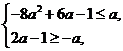
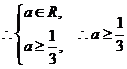 .
.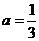 . ………………………………………………………………9分
. ………………………………………………………………9分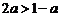 ,且
,且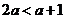 时,即
时,即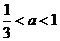 ,
,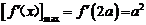 .
.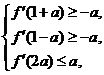 即
即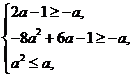
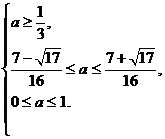 ∴
∴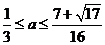 .
.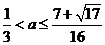 . ………………………………………………12分
. ………………………………………………12分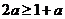 时,得
时,得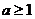 与已知
与已知 . ………………………14分
. ………………………14分 .
.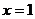 为
为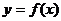 的图象在点(
的图象在点(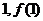 )处的切线方程为
)处的切线方程为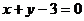 ,求
,求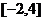 上的最大值;
上的最大值;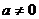 时,若
时,若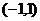 上不单调,求
上不单调,求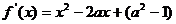 ……………………1分
……………………1分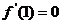 ,即
,即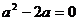 , ……………………2分
, ……………………2分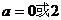 .
……………………4分
.
……………………4分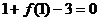 ∴
∴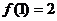 ……………………5分
……………………5分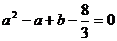
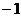 ,
,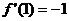 ,即
,即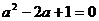 ,
∴
,
∴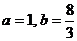 ……………………7分
……………………7分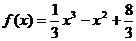
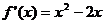 ,可知
,可知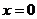 和
和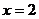 是
是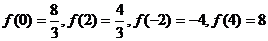 ……………………9分
……………………9分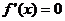 的两根为
的两根为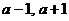 ,区间长为
,区间长为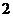 ,
,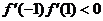 即:
即: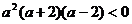 ……………………12分
……………………12分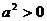 , ∴
, ∴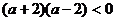 ,
,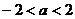
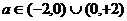 .
……………………13分
.
……………………13分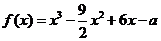 .
.
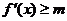 恒成立,求
恒成立,求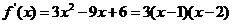 ,
,
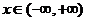 ,
,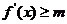 ,
即
,
即 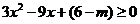 恒成立,
恒成立, 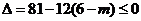 , 得
, 得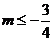 ,即
,即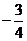
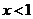 时,
时, 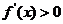 ;当
;当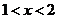 时,
时, 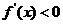 ;当
;当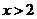 时,
时, 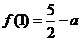 ;
;
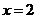 时,
时,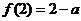 ;
;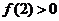 或
或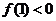 时, 方程
时, 方程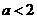 或
或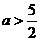 .
.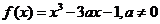
 求
求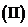 若
若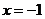 处取得极值,直线y=my与
处取得极值,直线y=my与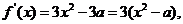
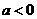 时,对
时,对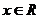 ,有
,有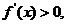
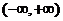
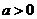 时,由
时,由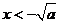 或
或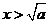 ;
;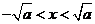 ,
,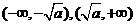 ;
;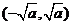 。
。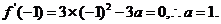
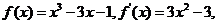
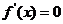 解得
解得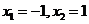 。
。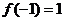 ,
,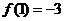 。
。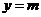 与函数
与函数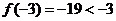 ,
,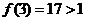 ,
,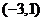 。
。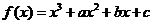 在
在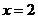 处都取得极值.
处都取得极值.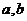 的值及函数
的值及函数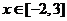 ,不等式
,不等式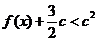 恒成立,求
恒成立,求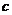 的取值范围.
的取值范围.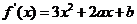 ,由题意:
,由题意: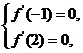 即
即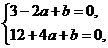 解得
解得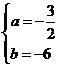
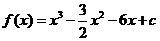 ,
,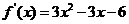
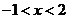 ;
;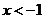 或
或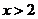 ,
,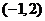 ;增区间为
;增区间为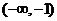 ,
,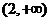 .---------------5分
.---------------5分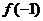 与
与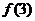 中的较大者.
中的较大者.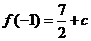 ;
; 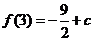
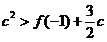 ,即:
,即: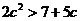
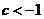 或
或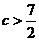 .
.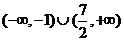 . -------------14分
. -------------14分