摘要：已知函数 (Ⅰ)为定义域上的单调函数.求实数的取值范围, (Ⅱ)当时.求函数的最大值, (Ⅲ)当时.且.证明:. 解:(1). ∴ 因为对.有 ∴不存在实数使.对恒成立 ---2分 由恒成立.∴.而.所以 经检验.当时.对恒成立. ∴当时.为定义域上的单调增函数 ---4分 (2)当时.由.得 当时..当时. ∴在时取得最大值.∴此时函数的最大值为 ---7分 得.对恒成立.当且仅当时取等号 当时..∵. ∴ ∴ 同理可得. ∴ ---12分 法二:当时(由待证命题的结构进行猜想.辅助函数.求差得之).在上递增 令 在上总有.即在上递增 当时..即 令由(2)它在上递减 ∴ 即. ∵ ∴.综上成立 ---12分
网址：http://m.1010jiajiao.com/timu_id_3935638[举报]
的定义域为
。
（其中
）不是函数
图像的切线；
上单调性，并证明；
满足
，求关于
的不等式
的解集
的定义域为
，且同时满足下列条件：（1）
求
的取值范围。
的定义域为
，且同时满足下列条件：（1）
求
的取值范围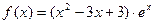 
的定义域为[－2，t](t>－2)，
在[－2，t]上为单调函数；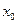
∈(－2，t)，满足
，
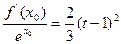的定义域为
，值域为
.下列关于函数
时，
；②将
，得到的图像必定是一条连续的曲线；③
上的单调函数；④