摘要:设 (Ⅰ)判断函数的单调性, (Ⅱ)是否存在实数.使得关于的不等式在(0.)上恒成立.若存在.求出的取值范围.若不存在.试说明理由, (Ⅲ)求证: (其中为自然对数的底数). 解:(Ⅱ)在上恒成立.在上恒成立. 设.则. ∴. 若.则时.恒成立. ∴在上为减函数 ∴在上恒成立.∴在上恒成立. 若显然不满足条件. 若.则时.. ∴时. ∴在上为增函数.当时..不能使在上恒成立. ∴ 可知在上恒成立.∴. 即. 取.即可证得对一切正整数成立.
网址:http://m.1010jiajiao.com/timu_id_3935637[举报]
已知函数![]() .
.
(1)判断函数f(x)的单调性,并说明理由;
(2)当t=0时,设y=f-1(x)为y=f(x)的反函数,令![]() ,是否存在这样的实数b,使得不等式g(x)>-ax2+x+b对任意的
,是否存在这样的实数b,使得不等式g(x)>-ax2+x+b对任意的![]() 和任意的x∈(0,+∞)恒成立?若存在,求出b的取值范围;若不存在,说明理由.
和任意的x∈(0,+∞)恒成立?若存在,求出b的取值范围;若不存在,说明理由.
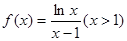
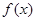 的单调性;
的单调性;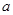 、使得关于
、使得关于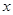 的不等式
的不等式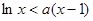 在(1,
在(1,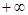 )上恒成立,若存在,求出
)上恒成立,若存在,求出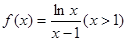
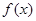 的单调性;
的单调性;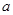 、使得关于
、使得关于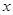 的不等式
的不等式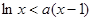 在(1,
在(1,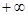 )上恒成立,若存在,求出
)上恒成立,若存在,求出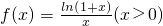
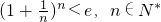 (其中e为自然对数的底数).
(其中e为自然对数的底数).