题目内容
16. 小金属球质量为m、用长L的轻悬线固定于O点,在O点的正下方$\frac{L}{2}$处钉有一颗钉子P,把悬线沿水平方向拉直,如图所示,无初速度释放小金属球,当悬线碰到钉子的瞬间(设线没有断),则( )
小金属球质量为m、用长L的轻悬线固定于O点,在O点的正下方$\frac{L}{2}$处钉有一颗钉子P,把悬线沿水平方向拉直,如图所示,无初速度释放小金属球,当悬线碰到钉子的瞬间(设线没有断),则( )| A. | 小球的角速度不变 | B. | 小球的线速度突然减小 | ||
| C. | 小球的向心加速度突然增大 | D. | 悬线的张力突然增大 |
分析 把悬线沿水平方向拉直后无初速度释放,当悬线碰到钉子的前后瞬间,线速度大小不变,半径发生变化,根据v=rω,a=$\frac{{v}^{2}}{r}$判断角速度、向心加速度大小的变化,再根据牛顿第二定律判断悬线拉力的变化
解答 解:A、把悬线沿水平方向拉直后无初速度释放,当悬线碰到钉子的前后瞬间,由于重力与拉力都与速度垂直,所以小球的线速度大小不变,根据v=rω,知线速度大小不变,半径变小,则角速度增大,故AB错误;
C、根据向心加速度公式a=$\frac{{v}^{2}}{r}$得线速度大小不变,半径变小,则向心加速度变大.故C正确;
D、根据牛顿第二定律得:T-mg=$\frac{{v}^{2}}{r}$得:T=mg+m$\frac{{v}^{2}}{r}$.半径变小,则拉力变大.故D正确.
故选:CD
点评 解决本题的关键知道线速度、角速度、向心加速度之间的关系,以及知道在本题中悬线碰到钉子的前后瞬间,线速度大小不变.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
7.要使两个质量分布均匀的小球间万有引力减小到原来的$\frac{1}{4}$,下列办法可行的是( )
| A. | 保持两小球的材料不变,使两小球的半径和距离均减少为原来的$\frac{1}{2}$ | |
| B. | 保持两小球的材料和距离不变,让两小球的半径变为原来的$\frac{1}{2}$ | |
| C. | 保持两小球的材料和半径不变,让两小球间的距离变为原来的2倍 | |
| D. | 保持两物体的材料不变,让两物体的半径和距离均变为原来的2倍 |
4.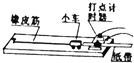 如图所示,在进行探究做功与速度关系的实验中,每次实验结束后要通过探究纸带上点来确定每次小车运动的最大速度,关于最大速度的测算描述正确的是( )
如图所示,在进行探究做功与速度关系的实验中,每次实验结束后要通过探究纸带上点来确定每次小车运动的最大速度,关于最大速度的测算描述正确的是( )
 如图所示,在进行探究做功与速度关系的实验中,每次实验结束后要通过探究纸带上点来确定每次小车运动的最大速度,关于最大速度的测算描述正确的是( )
如图所示,在进行探究做功与速度关系的实验中,每次实验结束后要通过探究纸带上点来确定每次小车运动的最大速度,关于最大速度的测算描述正确的是( )| A. | 利用开始纸带上打出的较为密集的点进行测算 | |
| B. | 利用中段纸带上打出的点进行测算 | |
| C. | 利用纸带上打下的从开始到最后的所有点进行测算 | |
| D. | 利用纸带上打出的间隔较为均匀分布的点进行测算 |
11. 如图所示,一理想变压器原线圈两端接频率为50Hz的正弦式交流电,R为电阻箱,现闭合开关S,调节电阻箱的阻值为18Ω时,恰好能使“36V 24W”的灯泡L1、L2正常发光,则( )
如图所示,一理想变压器原线圈两端接频率为50Hz的正弦式交流电,R为电阻箱,现闭合开关S,调节电阻箱的阻值为18Ω时,恰好能使“36V 24W”的灯泡L1、L2正常发光,则( )
 如图所示,一理想变压器原线圈两端接频率为50Hz的正弦式交流电,R为电阻箱,现闭合开关S,调节电阻箱的阻值为18Ω时,恰好能使“36V 24W”的灯泡L1、L2正常发光,则( )
如图所示,一理想变压器原线圈两端接频率为50Hz的正弦式交流电,R为电阻箱,现闭合开关S,调节电阻箱的阻值为18Ω时,恰好能使“36V 24W”的灯泡L1、L2正常发光,则( )| A. | 理想变压器原、副线圈的匝数比为4:1 | |
| B. | 该正弦式交流电电压瞬时值的表达式为u=144$\sqrt{2}$sin100πt(V) | |
| C. | 当灯泡L1、L2正常发光时,电阻箱R上消耗的电功率为72W | |
| D. | 断开开关S,将电阻箱调节为27Ω时,灯泡L1仍能正常发光 |
8. 质量为m的物体在水平恒定外力F作用下沿水平面做匀加速直线运动,一段时间后撤去外力,已知物体的v-t图象如图所示,则下列说法正确的有( )
质量为m的物体在水平恒定外力F作用下沿水平面做匀加速直线运动,一段时间后撤去外力,已知物体的v-t图象如图所示,则下列说法正确的有( )
 质量为m的物体在水平恒定外力F作用下沿水平面做匀加速直线运动,一段时间后撤去外力,已知物体的v-t图象如图所示,则下列说法正确的有( )
质量为m的物体在水平恒定外力F作用下沿水平面做匀加速直线运动,一段时间后撤去外力,已知物体的v-t图象如图所示,则下列说法正确的有( )| A. | 物体所受摩擦力大小为$\frac{m{v}_{0}}{2{t}_{0}}$ | |
| B. | 水平拉力大小是物体所受摩擦力大小的2倍 | |
| C. | 物体在加速段的平均速度大于减速段的平均速度 | |
| D. | 水平拉力大小是$\frac{3m{v}_{0}}{2{t}_{0}}$ |
12. 如图所示,光滑水平面AB与竖直面上的半圆形固定轨道在B点衔接,轨道半径为R,BC为直径.一可看作质点、质量为m的物块在A处压缩一轻质弹簧(物块与弹簧不连接),释放物块,物块被弹簧弹出后,经过半圆形轨道B点时对轨道的压力为其重力的7倍,之后向上运动并恰能通过半圆轨道的最高点C.不计空气阻力,重力加速度g=10m/s2.则( )
如图所示,光滑水平面AB与竖直面上的半圆形固定轨道在B点衔接,轨道半径为R,BC为直径.一可看作质点、质量为m的物块在A处压缩一轻质弹簧(物块与弹簧不连接),释放物块,物块被弹簧弹出后,经过半圆形轨道B点时对轨道的压力为其重力的7倍,之后向上运动并恰能通过半圆轨道的最高点C.不计空气阻力,重力加速度g=10m/s2.则( )
 如图所示,光滑水平面AB与竖直面上的半圆形固定轨道在B点衔接,轨道半径为R,BC为直径.一可看作质点、质量为m的物块在A处压缩一轻质弹簧(物块与弹簧不连接),释放物块,物块被弹簧弹出后,经过半圆形轨道B点时对轨道的压力为其重力的7倍,之后向上运动并恰能通过半圆轨道的最高点C.不计空气阻力,重力加速度g=10m/s2.则( )
如图所示,光滑水平面AB与竖直面上的半圆形固定轨道在B点衔接,轨道半径为R,BC为直径.一可看作质点、质量为m的物块在A处压缩一轻质弹簧(物块与弹簧不连接),释放物块,物块被弹簧弹出后,经过半圆形轨道B点时对轨道的压力为其重力的7倍,之后向上运动并恰能通过半圆轨道的最高点C.不计空气阻力,重力加速度g=10m/s2.则( )| A. | 物块经过B点时的速度的大小为$\sqrt{5gR}$ | |
| B. | 物块弹出前弹簧的弹性势能为3mgR | |
| C. | 物块在半圆轨道上克服阻力做功为$\frac{1}{3}$mgR | |
| D. | 若开始时弹簧的弹性势能为6mgR,则物块到达C点的动能小于$\frac{7}{2}$mgR |


