题目内容
7. 如图所示,三角形物块B放在倾角为θ的斜面体A上,A、B间的动摩擦因数为μ,要使B与A相对静止,已知A、B间的最大摩擦力等于滑动摩擦力,质量加速度为g,下列说法正确的是( )
如图所示,三角形物块B放在倾角为θ的斜面体A上,A、B间的动摩擦因数为μ,要使B与A相对静止,已知A、B间的最大摩擦力等于滑动摩擦力,质量加速度为g,下列说法正确的是( )| A. | 如果μ≠0且A、B相对地面静止,则μ可能小于tanθ | |
| B. | 如果μ≠0且A、B相对地面静止,则μ一定等于tanθ | |
| C. | 如果μ=0且用力推A使A、B共同向右加速,则加速度a一定大于gtanθ | |
| D. | 如果μ=0且用力推A使A、B共同向右加速,则加速度a=gtanθ |
分析 如果μ≠0且A、B相对地面静止,以B为研究对象,结合共点力的平衡即可求出;
如果μ=0且用力推A使A、B共同向右加速,则B沿水平方向做加速运动,竖直方向的合外力为0,结合牛顿第二定律与力的合成与分解即可求出.
解答 解:A、如果μ≠0且A、B相对地面静止,以B为研究对象,则根据题意:
μmgcosθ=mgsinθ
所以:$μ=\frac{sinθ}{cosθ}=tanθ$.故A错误,B正确.
C、如果μ=0,则B与A之间不存在摩擦力,用力推A使A、B共同向右加速时,B只受到重力和支持力的作用,受力如图,则:
由图可得:$\frac{ma}{mg}=tanθ$
则加速度a=gtanθ.故C错误,D正确.
故选:BD
点评 解决本题的关键能够正确地受力分析,抓住使A、B共同向右加速的条件,运用牛顿第二定律进行求解,注意整体法和隔离法的运用.

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
15.全球通信离不开人造卫星,同步卫星是最好的空间中继站,那么关于同步卫星以下叙述正确的是( )
| A. | 同步卫星运行的速度是7.9km/s | |
| B. | 同步卫星绕地球南北极转动 | |
| C. | 同步卫星只能在赤道平面内固定高度运行 | |
| D. | 不同轨道上都可以放置同步卫星 |
2.关于作用力、反作用力做功以下描述正确的是( )
| A. | 作用力、反作用力做功总是大小相等,且一正一负 | |
| B. | 作用力、反作用力总功总是一正一负,但大小可以不相等 | |
| C. | 不可能作用力、反作用力都做正功 | |
| D. | 作用力、反作用力可以一个力做功,另一个力不做功 |
12.在物理学的发展过程中,科学的物理思想与方法对物理学的发展起到了重要作用,下列关于物理思想和方法说法正确的是( )
| A. | 质点和点电荷是同一种思想方法 | |
| B. | 重心、合力都体现了等效思想 | |
| C. | 伽利略用小球在斜面上的运动验证了速度与位移成正比 | |
| D. | 牛顿第一定律是利用逻辑思维对事实进行分析的产物,不可能用实验直接证明 |
19. 若金星和地球的公转轨道均视为圆形,且在同一平面内,如图所示.在地球上观测,发现金星与太阳可呈现的视角(太阳与金星均视为质点,它们与眼睛连线的夹角)有最大值,最大视角的正弦值为k,则金星的公转周期为( )
若金星和地球的公转轨道均视为圆形,且在同一平面内,如图所示.在地球上观测,发现金星与太阳可呈现的视角(太阳与金星均视为质点,它们与眼睛连线的夹角)有最大值,最大视角的正弦值为k,则金星的公转周期为( )
 若金星和地球的公转轨道均视为圆形,且在同一平面内,如图所示.在地球上观测,发现金星与太阳可呈现的视角(太阳与金星均视为质点,它们与眼睛连线的夹角)有最大值,最大视角的正弦值为k,则金星的公转周期为( )
若金星和地球的公转轨道均视为圆形,且在同一平面内,如图所示.在地球上观测,发现金星与太阳可呈现的视角(太阳与金星均视为质点,它们与眼睛连线的夹角)有最大值,最大视角的正弦值为k,则金星的公转周期为( )| A. | $(1-{k}^{2})^{\frac{3}{2}}$年 | B. | $(1-{k}^{2})^{\frac{3}{4}}$年 | C. | k3年 | D. | $\sqrt{{k}^{3}}$年 |
16. 如图所示,质量为m的小物块从A处由静止开始沿倾角为θ的光滑斜面AO下滑,进入粗糙水平面继续滑动,最终停在B处.已知A距水平面OB的高度为物块与水平面间的动摩擦因数恒为μ,重力加速度大小为g.则( )
如图所示,质量为m的小物块从A处由静止开始沿倾角为θ的光滑斜面AO下滑,进入粗糙水平面继续滑动,最终停在B处.已知A距水平面OB的高度为物块与水平面间的动摩擦因数恒为μ,重力加速度大小为g.则( )
 如图所示,质量为m的小物块从A处由静止开始沿倾角为θ的光滑斜面AO下滑,进入粗糙水平面继续滑动,最终停在B处.已知A距水平面OB的高度为物块与水平面间的动摩擦因数恒为μ,重力加速度大小为g.则( )
如图所示,质量为m的小物块从A处由静止开始沿倾角为θ的光滑斜面AO下滑,进入粗糙水平面继续滑动,最终停在B处.已知A距水平面OB的高度为物块与水平面间的动摩擦因数恒为μ,重力加速度大小为g.则( )| A. | O、B两点间的距离为$\frac{h}{μ}$ | |
| B. | O、B两点间的距离为μh | |
| C. | 物块滑到斜面底端时重力的功率为mg$\sqrt{2gh}$ | |
| D. | 物块滑到斜面底端时重力的功率为mg$\sqrt{2gh}$cosθ |
17.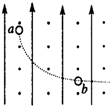 如图所示,在空间存在着水平方向的匀强磁场和竖直方向的匀强电场.电场强度为E,磁感应强度为B,在某点由静止释放一个带电液滴a,它运动到最低点处,恰与一个原来悬浮于图示位置的液滴b相撞.撞后两液滴合为一体,以原速的$\frac{2}{3}$沿水平方向做直线运动.已知液滴a质量是液滴b质量m的2倍,液滴a所带电荷量是液滴b所带电荷量q的4倍.则a、b的带电性质和初始位置之间的高度差h为(设a、b之间的静电力可以不计,重力加速度为g)( )
如图所示,在空间存在着水平方向的匀强磁场和竖直方向的匀强电场.电场强度为E,磁感应强度为B,在某点由静止释放一个带电液滴a,它运动到最低点处,恰与一个原来悬浮于图示位置的液滴b相撞.撞后两液滴合为一体,以原速的$\frac{2}{3}$沿水平方向做直线运动.已知液滴a质量是液滴b质量m的2倍,液滴a所带电荷量是液滴b所带电荷量q的4倍.则a、b的带电性质和初始位置之间的高度差h为(设a、b之间的静电力可以不计,重力加速度为g)( )
 如图所示,在空间存在着水平方向的匀强磁场和竖直方向的匀强电场.电场强度为E,磁感应强度为B,在某点由静止释放一个带电液滴a,它运动到最低点处,恰与一个原来悬浮于图示位置的液滴b相撞.撞后两液滴合为一体,以原速的$\frac{2}{3}$沿水平方向做直线运动.已知液滴a质量是液滴b质量m的2倍,液滴a所带电荷量是液滴b所带电荷量q的4倍.则a、b的带电性质和初始位置之间的高度差h为(设a、b之间的静电力可以不计,重力加速度为g)( )
如图所示,在空间存在着水平方向的匀强磁场和竖直方向的匀强电场.电场强度为E,磁感应强度为B,在某点由静止释放一个带电液滴a,它运动到最低点处,恰与一个原来悬浮于图示位置的液滴b相撞.撞后两液滴合为一体,以原速的$\frac{2}{3}$沿水平方向做直线运动.已知液滴a质量是液滴b质量m的2倍,液滴a所带电荷量是液滴b所带电荷量q的4倍.则a、b的带电性质和初始位置之间的高度差h为(设a、b之间的静电力可以不计,重力加速度为g)( )| A. | a带负电,b带正电 | B. | a带正电,b带正电 | C. | h=$\frac{3{m}^{2}g}{2{B}^{2}{q}^{2}}$ | D. | h=$\frac{2{m}^{2}g}{3{B}^{2}{q}^{2}}$ |

 如图所示,所有轨道均光滑,轨道AB与水平面的夹角为θ=37°,A点距水平轨道的高度为H=1.8m.一无动力小滑车质量为m=1.0kg,从A点沿轨道由静止滑下,经过水平轨道BC再滑入圆形轨道内侧,圆形轨道半径R=0.5m,通过圆形轨道最高点D然后从水平轨道E点飞出,E点右侧有一壕沟,E、F两点的竖直高度差h=1.25m,水平距离s=2.6m.不计小滑车通过B点时的能量损失,小滑车在运动全过程中可视为质点,g=10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,所有轨道均光滑,轨道AB与水平面的夹角为θ=37°,A点距水平轨道的高度为H=1.8m.一无动力小滑车质量为m=1.0kg,从A点沿轨道由静止滑下,经过水平轨道BC再滑入圆形轨道内侧,圆形轨道半径R=0.5m,通过圆形轨道最高点D然后从水平轨道E点飞出,E点右侧有一壕沟,E、F两点的竖直高度差h=1.25m,水平距离s=2.6m.不计小滑车通过B点时的能量损失,小滑车在运动全过程中可视为质点,g=10m/s2,sin37°=0.6,cos37°=0.8,求: