题目内容
12.在物理学的发展过程中,科学的物理思想与方法对物理学的发展起到了重要作用,下列关于物理思想和方法说法正确的是( )| A. | 质点和点电荷是同一种思想方法 | |
| B. | 重心、合力都体现了等效思想 | |
| C. | 伽利略用小球在斜面上的运动验证了速度与位移成正比 | |
| D. | 牛顿第一定律是利用逻辑思维对事实进行分析的产物,不可能用实验直接证明 |
分析 质点及点电荷采用了理想化的物理模型的方法.合力与分力能够等效替代,采用了等效替代的思想;伽利略提出了“落体运动的速度v与时间t成正比”的观点.不受力的实验只能是理想实验,是无任何实验误差的思维实验,严格来说“不受力”的条件真实实验不能满足.
解答 解:A、质点及点电荷采用了理想化的物理模型的方法,所以质点和点电荷是同一种思想方法,故A正确;
B、重心、合力和分力、总电阻都采用了等效替代的思想,故B正确;
C、伽利略提出了“落体运动的速度v与时间t成正比”的观点,不是速度跟位移成正比,故C错误;
D、不受力的实验只能是理想实验,是无任何实验误差的思维实验,严格来说“不受力”的条件真实实验不能满足,只能靠思维的逻辑推理去把握,故牛顿第一定律是不可以通过实验直接得以验证的,故D正确;
故选:ABD.
点评 对于物理学上重要的实验和发现,可根据实验的原理、内容、结论及相应的物理学家等等一起记忆,不能混淆.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
3.一学生用细绳拉一物体在水平地面上沿着圆弧曲线由P点匀速率运动到Q点.已知物体与地面之间的摩擦阻力方向与物体方向相反,则下列画出的细绳的拉力F的方向(在地面所在的平面内)可能正确的是( )
| A. |  | B. |  | C. |  | D. |  |
20.质点做变速直线运动的v-t图象如图所示,关于质点的运动下列判断正确的是( )


| A. | 质点做的是初速度为v0的匀加速运动 | |
| B. | 质点做的是加速度逐渐增大的变加速运动,位移大于$\frac{{v}_{0}+v}{2}$t | |
| C. | 质点做的是加速度逐渐减小的变加速运动,位移小于$\frac{{v}_{0}+v}{2}$t | |
| D. | 质点做的是加速度逐渐减小的变加速运动,位移大于$\frac{{v}_{0}+v}{2}$t |
7. 如图所示,三角形物块B放在倾角为θ的斜面体A上,A、B间的动摩擦因数为μ,要使B与A相对静止,已知A、B间的最大摩擦力等于滑动摩擦力,质量加速度为g,下列说法正确的是( )
如图所示,三角形物块B放在倾角为θ的斜面体A上,A、B间的动摩擦因数为μ,要使B与A相对静止,已知A、B间的最大摩擦力等于滑动摩擦力,质量加速度为g,下列说法正确的是( )
 如图所示,三角形物块B放在倾角为θ的斜面体A上,A、B间的动摩擦因数为μ,要使B与A相对静止,已知A、B间的最大摩擦力等于滑动摩擦力,质量加速度为g,下列说法正确的是( )
如图所示,三角形物块B放在倾角为θ的斜面体A上,A、B间的动摩擦因数为μ,要使B与A相对静止,已知A、B间的最大摩擦力等于滑动摩擦力,质量加速度为g,下列说法正确的是( )| A. | 如果μ≠0且A、B相对地面静止,则μ可能小于tanθ | |
| B. | 如果μ≠0且A、B相对地面静止,则μ一定等于tanθ | |
| C. | 如果μ=0且用力推A使A、B共同向右加速,则加速度a一定大于gtanθ | |
| D. | 如果μ=0且用力推A使A、B共同向右加速,则加速度a=gtanθ |
17. 氢原子能级的示意图如图所示,大量氢原子从n=4的能级向n=2的能级跃迁时辐射处可见光a,从n=3的能级向n=2的能级跃迁时辐射处可见光b,则( )
氢原子能级的示意图如图所示,大量氢原子从n=4的能级向n=2的能级跃迁时辐射处可见光a,从n=3的能级向n=2的能级跃迁时辐射处可见光b,则( )
 氢原子能级的示意图如图所示,大量氢原子从n=4的能级向n=2的能级跃迁时辐射处可见光a,从n=3的能级向n=2的能级跃迁时辐射处可见光b,则( )
氢原子能级的示意图如图所示,大量氢原子从n=4的能级向n=2的能级跃迁时辐射处可见光a,从n=3的能级向n=2的能级跃迁时辐射处可见光b,则( )| A. | a光的光子能量大于b光的光子能量 | |
| B. | 氢原子从n=4的能级向n=3的能级跃迁时会辐射处紫外线 | |
| C. | 处于能级n=4的电子的动能小于能级n=2的动能 | |
| D. | 在真空中传播时,b光的波长较短 | |
| E. | 处在n=1能级时核外电子离原子核最近 |
4. 如图所示,曲线MN为某磁场中的一磁感应线,A、B为该磁感应线上的两点,则下列判断中正确的是( )
如图所示,曲线MN为某磁场中的一磁感应线,A、B为该磁感应线上的两点,则下列判断中正确的是( )
 如图所示,曲线MN为某磁场中的一磁感应线,A、B为该磁感应线上的两点,则下列判断中正确的是( )
如图所示,曲线MN为某磁场中的一磁感应线,A、B为该磁感应线上的两点,则下列判断中正确的是( )| A. | 该磁感线有可能是匀强磁场的磁感线 | |
| B. | 若一小段通电导线在A点受到的安培力大于其在B点受到的安培力,则A点的磁感应强度一定大于B点的磁感应强度大小 | |
| C. | 若在A点由静止释放一个点电荷,则该点电荷在A点时的加速度方向一定沿A点的切线方向 | |
| D. | 若将小磁针分别放置在A、B两点,则小磁针静止时N极的指向一定沿A、B两点的切线方向 |
2.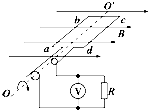 如图所示为小型旋转电枢式交流发电机的原理图,其矩形线圈在磁感应强度为B的匀强磁场中绕垂直于磁场方向的固定轴OO′以角速度ω匀速转动,线圈的面积为S、匝数为n、线圈总电阻为r,线圈的两端经集流环和电刷与电阻R连接,与电阻R并联的交流电压表为理想电表.在t=0时刻,线圈平面与磁场方向平行,则下列说法正确的是( )
如图所示为小型旋转电枢式交流发电机的原理图,其矩形线圈在磁感应强度为B的匀强磁场中绕垂直于磁场方向的固定轴OO′以角速度ω匀速转动,线圈的面积为S、匝数为n、线圈总电阻为r,线圈的两端经集流环和电刷与电阻R连接,与电阻R并联的交流电压表为理想电表.在t=0时刻,线圈平面与磁场方向平行,则下列说法正确的是( )
 如图所示为小型旋转电枢式交流发电机的原理图,其矩形线圈在磁感应强度为B的匀强磁场中绕垂直于磁场方向的固定轴OO′以角速度ω匀速转动,线圈的面积为S、匝数为n、线圈总电阻为r,线圈的两端经集流环和电刷与电阻R连接,与电阻R并联的交流电压表为理想电表.在t=0时刻,线圈平面与磁场方向平行,则下列说法正确的是( )
如图所示为小型旋转电枢式交流发电机的原理图,其矩形线圈在磁感应强度为B的匀强磁场中绕垂直于磁场方向的固定轴OO′以角速度ω匀速转动,线圈的面积为S、匝数为n、线圈总电阻为r,线圈的两端经集流环和电刷与电阻R连接,与电阻R并联的交流电压表为理想电表.在t=0时刻,线圈平面与磁场方向平行,则下列说法正确的是( )| A. | 交流发电机产生的电动势的最大值Em=nBSω | |
| B. | 交流电压表的示数为$\frac{\sqrt{2}nRBSω}{2(R+r)}$ | |
| C. | 线圈从t=0时刻开始转过90°的过程中,通过电阻的电荷量为$\frac{πnBS}{2\sqrt{2}(R+r)}$ | |
| D. | 线圈从t=0时刻开始转过90°的过程中,电阻产生的热量为$\frac{2{n}^{2}ωR{B}^{2}{S}^{2}}{π(R+r)}$ |
 如图所示,质量为m=2kg的木块在倾角θ=37°的斜面上由静止开始下滑(斜面足够长),木块在斜面上所受的摩擦力为8N(sin37°=0.6,cos37°=0.8)求:
如图所示,质量为m=2kg的木块在倾角θ=37°的斜面上由静止开始下滑(斜面足够长),木块在斜面上所受的摩擦力为8N(sin37°=0.6,cos37°=0.8)求: