题目内容
19. 如图,质量分别为M和m的两物块与竖直轻弹簧相连,放在水平面上处于静止状态.现将m竖直向下压缩弹簧一段距离后由静止释放,当m到达最高点时,M恰好对地面无压力.已知弹簧劲度系数为k,弹簧形变始终在弹性限度内,重力加速度为g,则( )
如图,质量分别为M和m的两物块与竖直轻弹簧相连,放在水平面上处于静止状态.现将m竖直向下压缩弹簧一段距离后由静止释放,当m到达最高点时,M恰好对地面无压力.已知弹簧劲度系数为k,弹簧形变始终在弹性限度内,重力加速度为g,则( )| A. | 当m到达最高点时,m的加速度为(1+$\frac{M}{m}$)g | |
| B. | 当m到达最高点时,M的加速度为g | |
| C. | 当m速度最大时,弹簧的形变最为$\frac{Mg}{k}$ | |
| D. | 当m速度最大时,M对地面的压力为(M+m)g |
分析 当m到达最高点时,M恰好对地面无压力.此时M受到的弹簧的拉力等于M的重力,再对m受力分析,根据牛顿第二定律求得加速度,当m速度最大时,m的加速度为0,由平衡条件和胡克定律求弹簧的形变量.并求M对地面的压力.
解答 解:A、当m到达最高点时,M恰好对地面无压力,则知弹簧对M的拉力 F=Mg,所以弹簧对m的作用力也是Mg,所以m的加速度为:
am=$\frac{mg+Mg}{m}$=(1+$\frac{M}{m}$)g.故A正确;
B、当m到达最高点时,M刚好对地面没有压力,可知弹簧对M的拉力为Mg,M受到的合力为零,加速度为零,故B错误;
C、开始时弹簧对m的弹力大于m的重力,m向上做加速运动,当弹簧的弹力小于m的重力时,m向上做减速运动,所以弹簧中弹力等于mg时m速度最大,由胡克定律得:mg=kx,得:弹簧的形变量 x=$\frac{mg}{k}$.故C错误;
D、当m速度最大时,对M受力分析得 FN-kx-Mg=0,解得FN=(M+m)g.由牛顿第三定律知,M对地面的压力为(M+m)g.故D正确.
故选:AD
点评 本题主要考查了弹簧的弹力对Mm的运动分析,关键是抓住当m处于最高点时,M刚好要离开地面时弹簧的弹力等于M的重力.当m速度最大时,m的加速度为0.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
2.关于功率公式P=$\frac{W}{t}$t和P=Fv,下列说法正确的有( )
| A. | 据P=$\frac{W}{t}$,知道W和t就可求出任意时刻的功率 | |
| B. | 据P=$\frac{W}{t}$,知道W和t就可求出t内的平均功率 | |
| C. | 从P=Fv知,汽车的功率一定与它的速度成正比 | |
| D. | 从P=Fv知,当功率一定时,牵引力与速度成反比 |
10.如图a,物体在水平恒力F作用下沿粗糙水平地面由静止开始运动,在t=1s时刻撤去恒力F.物体运动的v-t图象如图b.重力加速度g=10m/s2,则( )
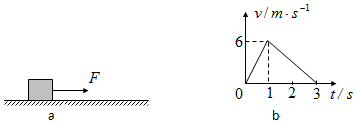
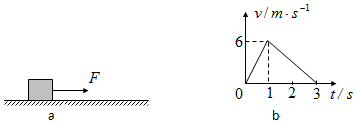
| A. | 物体在3s内的位移s=3m | |
| B. | 恒力F与摩擦力f大小之比F:f=3:1 | |
| C. | 物体与地面的动摩擦因数为μ=0.3 | |
| D. | 3s内恒力做功WF与克服摩擦力做功Wf之比WF:Wf=3:2 |
7.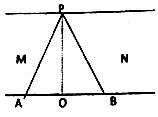 如图所示,MN是流速稳定的河流,水流方向M到N,船在静水中的速度为v,自河一岸的P点开始渡河,第一次船沿PA航行,第二次船沿PB航行,若PA、PB跟河岸垂线PO的夹角相等,两次航行所用的时间分别为TA和TB,则( )
如图所示,MN是流速稳定的河流,水流方向M到N,船在静水中的速度为v,自河一岸的P点开始渡河,第一次船沿PA航行,第二次船沿PB航行,若PA、PB跟河岸垂线PO的夹角相等,两次航行所用的时间分别为TA和TB,则( )
 如图所示,MN是流速稳定的河流,水流方向M到N,船在静水中的速度为v,自河一岸的P点开始渡河,第一次船沿PA航行,第二次船沿PB航行,若PA、PB跟河岸垂线PO的夹角相等,两次航行所用的时间分别为TA和TB,则( )
如图所示,MN是流速稳定的河流,水流方向M到N,船在静水中的速度为v,自河一岸的P点开始渡河,第一次船沿PA航行,第二次船沿PB航行,若PA、PB跟河岸垂线PO的夹角相等,两次航行所用的时间分别为TA和TB,则( )| A. | TA>TB | B. | TA<TB | ||
| C. | TA=TB | D. | 无法比较TA和TB的大小 |
11. 如图,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的,不计空气阻力,则( )
如图,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的,不计空气阻力,则( )
 如图,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的,不计空气阻力,则( )
如图,x轴在水平地面内,y轴沿竖直方向.图中画出了从y轴上沿x轴正向抛出的三个小球a、b和c的运动轨迹,其中b和c是从同一点抛出的,不计空气阻力,则( )| A. | a的飞行时间比b的短 | B. | b和c的飞行时间相同 | ||
| C. | a的水平速度比b的小 | D. | b的初速度比c的大 |
8.匀加速直线运动的物体的加速度为3m/s2,下列说法正确的是( )
| A. | 任意一秒末的速度总比前一秒初的速度大3m/s | |
| B. | 任意一秒初的速度总比前一秒末的速度大3m/s | |
| C. | 任意一秒的平均速度总比前一秒的平均速度大3m/s | |
| D. | 任意一秒内发生的位移总比前一秒发生的位移大3m |
 车在水平专用测试道上进行测试,该车总质量为m=1×103 kg,由静止开始沿水平测试道运动.传感设备记录其运动的速度时间图象(v-t图象)如图所示.该车运动中受到的阻力(含空气阻力)恒定,且阻力与车对路面压力的比值为μ=0.2.赛车在0~5s的v-t图象为直线,5s末达到该车发动机的额定牵引功率并保持该功率行驶,在5s~50s之间,赛车的v-t图象是一段曲线,50s以后为直线.取g取10m/s2,求:
车在水平专用测试道上进行测试,该车总质量为m=1×103 kg,由静止开始沿水平测试道运动.传感设备记录其运动的速度时间图象(v-t图象)如图所示.该车运动中受到的阻力(含空气阻力)恒定,且阻力与车对路面压力的比值为μ=0.2.赛车在0~5s的v-t图象为直线,5s末达到该车发动机的额定牵引功率并保持该功率行驶,在5s~50s之间,赛车的v-t图象是一段曲线,50s以后为直线.取g取10m/s2,求: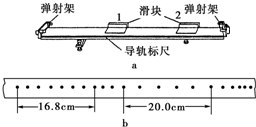 某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验,气垫导轨装置如图(a)所示,它由导轨、滑块、弹射架等组成.在空腔导轨的两个工作面上均匀分布着一定数量的小孔,向导轨空腔内不断通入压缩空气,空气会从小孔中喷出,使滑块稳定地漂浮在导轨上,这样就大大减小了因滑块和导轨之间的摩擦而引起的误差.
某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验,气垫导轨装置如图(a)所示,它由导轨、滑块、弹射架等组成.在空腔导轨的两个工作面上均匀分布着一定数量的小孔,向导轨空腔内不断通入压缩空气,空气会从小孔中喷出,使滑块稳定地漂浮在导轨上,这样就大大减小了因滑块和导轨之间的摩擦而引起的误差.