题目内容
4.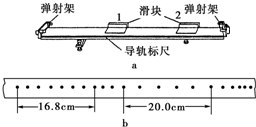 某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验,气垫导轨装置如图(a)所示,它由导轨、滑块、弹射架等组成.在空腔导轨的两个工作面上均匀分布着一定数量的小孔,向导轨空腔内不断通入压缩空气,空气会从小孔中喷出,使滑块稳定地漂浮在导轨上,这样就大大减小了因滑块和导轨之间的摩擦而引起的误差.
某同学利用打点计时器和气垫导轨做验证动量守恒定律的实验,气垫导轨装置如图(a)所示,它由导轨、滑块、弹射架等组成.在空腔导轨的两个工作面上均匀分布着一定数量的小孔,向导轨空腔内不断通入压缩空气,空气会从小孔中喷出,使滑块稳定地漂浮在导轨上,这样就大大减小了因滑块和导轨之间的摩擦而引起的误差.实验过程中测得弹射架弹射出的滑块1的质量310g,原来静止的滑块2(包括橡皮泥)的质量为205g,已知打点计时器每隔0.02s打一个点,计算可知两滑块相互作用以前系统的总动量为0.620kg•m/s;两滑块相互作用以后系统的总动量为0.618kg•m/s(保留三位有效数字).
分析 用打点计时器纸带的数据根据平均速度法测量碰前和碰后的速度,从而计算碰撞前后的动量大小.
解答 解:由图可知,碰前5段间隔内打点距离为x1=20.0cm=0.200m;
作用前系统的总动量为滑块1的动量,
p0=m1v0,v0=$\frac{0.2}{0.1}$ m/s=2 m/s,
p0=0.310×2 kg•m/s=0.620 kg•m/s.
作用后系统的总动量为滑块1和滑块2的动量和,且此时两滑块具有相同的速度v,碰后5段打点间隔内距离为x2=16.8cm=0.168m;
解得:v=$\frac{0.168}{0.14}$ m/s=1.2 m/s,
p=(m1+m2)v=(0.310+0.205)×1.2 kg•m/s=0.618 kg•m/s.
故答案为:0.620;0.618.
点评 本题考查用打点计时器验证动量守恒定律的方法; 解题时要注意明确实验原理,明确利用平均速度方法求解速度的方法,同时确定动量大小.

练习册系列答案
相关题目
7. 如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则( )
如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则( )
 如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则( )
如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则( )| A. | b、c向心加速度相等,且大于a的向心加速度 | |
| B. | b所需向心力最大 | |
| C. | b、c的线速度大小相等,且大于a的线速度 | |
| D. | b、c周期相等,且大于a的周期 |
19. 如图,质量分别为M和m的两物块与竖直轻弹簧相连,放在水平面上处于静止状态.现将m竖直向下压缩弹簧一段距离后由静止释放,当m到达最高点时,M恰好对地面无压力.已知弹簧劲度系数为k,弹簧形变始终在弹性限度内,重力加速度为g,则( )
如图,质量分别为M和m的两物块与竖直轻弹簧相连,放在水平面上处于静止状态.现将m竖直向下压缩弹簧一段距离后由静止释放,当m到达最高点时,M恰好对地面无压力.已知弹簧劲度系数为k,弹簧形变始终在弹性限度内,重力加速度为g,则( )
 如图,质量分别为M和m的两物块与竖直轻弹簧相连,放在水平面上处于静止状态.现将m竖直向下压缩弹簧一段距离后由静止释放,当m到达最高点时,M恰好对地面无压力.已知弹簧劲度系数为k,弹簧形变始终在弹性限度内,重力加速度为g,则( )
如图,质量分别为M和m的两物块与竖直轻弹簧相连,放在水平面上处于静止状态.现将m竖直向下压缩弹簧一段距离后由静止释放,当m到达最高点时,M恰好对地面无压力.已知弹簧劲度系数为k,弹簧形变始终在弹性限度内,重力加速度为g,则( )| A. | 当m到达最高点时,m的加速度为(1+$\frac{M}{m}$)g | |
| B. | 当m到达最高点时,M的加速度为g | |
| C. | 当m速度最大时,弹簧的形变最为$\frac{Mg}{k}$ | |
| D. | 当m速度最大时,M对地面的压力为(M+m)g |
9.跳水运动员从10m跳台上下落的过程中,重力做功和重力势能变化的情况( )
| A. | 重力做正功,重力势能增大 | B. | 重力做正功,重力势能减小 | ||
| C. | 重力做负功,重力势能增大 | D. | 重力做负功,重力势能减小 |
16. 在光滑圆锥形容器中,固定了一根光滑的竖直细杆,细杆与圆锥的中轴线重合,细杆上穿有小环(小环可以自由转动,但不能上下移动),小环上连接一轻绳,与一质量为m的光滑小球相连,让小球在圆锥内做水平面上的匀速圆周运动,并与圆锥内壁接触.如图所示,图a中小环与小球在同一水平面上,图b中轻绳与竖直轴成θ(θ<90°)角.设图a和图b中轻绳对小球的拉力分别为Ta和Tb,圆锥内壁对小球的支持力分别为Na和Nb,则在下列说法中正确的是( )
在光滑圆锥形容器中,固定了一根光滑的竖直细杆,细杆与圆锥的中轴线重合,细杆上穿有小环(小环可以自由转动,但不能上下移动),小环上连接一轻绳,与一质量为m的光滑小球相连,让小球在圆锥内做水平面上的匀速圆周运动,并与圆锥内壁接触.如图所示,图a中小环与小球在同一水平面上,图b中轻绳与竖直轴成θ(θ<90°)角.设图a和图b中轻绳对小球的拉力分别为Ta和Tb,圆锥内壁对小球的支持力分别为Na和Nb,则在下列说法中正确的是( )
 在光滑圆锥形容器中,固定了一根光滑的竖直细杆,细杆与圆锥的中轴线重合,细杆上穿有小环(小环可以自由转动,但不能上下移动),小环上连接一轻绳,与一质量为m的光滑小球相连,让小球在圆锥内做水平面上的匀速圆周运动,并与圆锥内壁接触.如图所示,图a中小环与小球在同一水平面上,图b中轻绳与竖直轴成θ(θ<90°)角.设图a和图b中轻绳对小球的拉力分别为Ta和Tb,圆锥内壁对小球的支持力分别为Na和Nb,则在下列说法中正确的是( )
在光滑圆锥形容器中,固定了一根光滑的竖直细杆,细杆与圆锥的中轴线重合,细杆上穿有小环(小环可以自由转动,但不能上下移动),小环上连接一轻绳,与一质量为m的光滑小球相连,让小球在圆锥内做水平面上的匀速圆周运动,并与圆锥内壁接触.如图所示,图a中小环与小球在同一水平面上,图b中轻绳与竖直轴成θ(θ<90°)角.设图a和图b中轻绳对小球的拉力分别为Ta和Tb,圆锥内壁对小球的支持力分别为Na和Nb,则在下列说法中正确的是( )| A. | Ta一定为零,Tb一定为零 | |
| B. | Na不一定为零,Nb可以为零 | |
| C. | Ta、Tb是否为零取决于小球速度的大小 | |
| D. | Na、Nb的大小与小球的速度无关 |
13. 如图,一水平桌面上固定一半径为R的光滑半圆弧形轨道OQP,圆弧所对的圆心角为180°,在圆弧轨道最左端Q处安装一压力传感器,轨道O处切线与桌面边缘垂直,P处安装一弹簧枪,可发射质量为m的小球.已知重力加速度为g,桌面离水平地面的高度为h,若P处弹簧枪发射一质量为m的小球,运动到Q处时压力传感器的读数为F,则( )
如图,一水平桌面上固定一半径为R的光滑半圆弧形轨道OQP,圆弧所对的圆心角为180°,在圆弧轨道最左端Q处安装一压力传感器,轨道O处切线与桌面边缘垂直,P处安装一弹簧枪,可发射质量为m的小球.已知重力加速度为g,桌面离水平地面的高度为h,若P处弹簧枪发射一质量为m的小球,运动到Q处时压力传感器的读数为F,则( )
 如图,一水平桌面上固定一半径为R的光滑半圆弧形轨道OQP,圆弧所对的圆心角为180°,在圆弧轨道最左端Q处安装一压力传感器,轨道O处切线与桌面边缘垂直,P处安装一弹簧枪,可发射质量为m的小球.已知重力加速度为g,桌面离水平地面的高度为h,若P处弹簧枪发射一质量为m的小球,运动到Q处时压力传感器的读数为F,则( )
如图,一水平桌面上固定一半径为R的光滑半圆弧形轨道OQP,圆弧所对的圆心角为180°,在圆弧轨道最左端Q处安装一压力传感器,轨道O处切线与桌面边缘垂直,P处安装一弹簧枪,可发射质量为m的小球.已知重力加速度为g,桌面离水平地面的高度为h,若P处弹簧枪发射一质量为m的小球,运动到Q处时压力传感器的读数为F,则( )| A. | 发射的小球的速度为$\sqrt{\frac{FR}{m}}$ | |
| B. | 小球从发射到落地,运动的总时间$π\sqrt{\frac{mR}{F}}$ | |
| C. | 弹簧枪对小球做功为$\frac{FR}{2}$ | |
| D. | 小球落地点到桌子边缘的水平距离为$\sqrt{\frac{2FRh}{mg}}$ |
14. 如图枪管AB对准小球C,A、B、C在同一水平面上,枪管和小球距地面的高度为45m.已知BC=100m,当子弹射出枪口时的速度v0=50m/s时,子弹恰好能在C下落20m时击中C.现其他条件不变,只改变子弹射出枪口时的速度v0,则(不计空气阻力,取g=10m/s2)( )
如图枪管AB对准小球C,A、B、C在同一水平面上,枪管和小球距地面的高度为45m.已知BC=100m,当子弹射出枪口时的速度v0=50m/s时,子弹恰好能在C下落20m时击中C.现其他条件不变,只改变子弹射出枪口时的速度v0,则(不计空气阻力,取g=10m/s2)( )
 如图枪管AB对准小球C,A、B、C在同一水平面上,枪管和小球距地面的高度为45m.已知BC=100m,当子弹射出枪口时的速度v0=50m/s时,子弹恰好能在C下落20m时击中C.现其他条件不变,只改变子弹射出枪口时的速度v0,则(不计空气阻力,取g=10m/s2)( )
如图枪管AB对准小球C,A、B、C在同一水平面上,枪管和小球距地面的高度为45m.已知BC=100m,当子弹射出枪口时的速度v0=50m/s时,子弹恰好能在C下落20m时击中C.现其他条件不变,只改变子弹射出枪口时的速度v0,则(不计空气阻力,取g=10m/s2)( )| A. | v0=34 m/s时,子弹能击中小球 | |
| B. | v0=32 m/s时,子弹能击中小球 | |
| C. | v0=30 m/s时,子弹能击中小球 | |
| D. | 以上的三个v0值,子弹可能都不能击中小球 |
 如图所示,矩形盒B的质量为M=5m,底部长度为L,放在水平面上,盒内有一质量为m可视为质点的物体A,A与B、B与地面间的动摩擦因数均为μ,开始时二者均静止,A在B的左端.现瞬间使物体A获得一向右的水平初速度v0,以后物体A与盒B的左右壁碰撞时,B始终向右运动,且每次碰撞时间均极短.当A与B的左壁最后一次碰撞后,B立刻停止运动,A继续向右滑行距离s(s<L)后也停止运动,已知滑动摩擦力等于最大静摩擦力.
如图所示,矩形盒B的质量为M=5m,底部长度为L,放在水平面上,盒内有一质量为m可视为质点的物体A,A与B、B与地面间的动摩擦因数均为μ,开始时二者均静止,A在B的左端.现瞬间使物体A获得一向右的水平初速度v0,以后物体A与盒B的左右壁碰撞时,B始终向右运动,且每次碰撞时间均极短.当A与B的左壁最后一次碰撞后,B立刻停止运动,A继续向右滑行距离s(s<L)后也停止运动,已知滑动摩擦力等于最大静摩擦力.