题目内容
7.我国1984年发射过一颗同步卫星,这颗卫星位于赤道上空相对地面静止不动,已知地球半径是R,质量是M,自转周期T,万有引力常量G,那么这颗卫星距地面高度的表达式是$\root{3}{\frac{GM{T}^{2}}{4{π}^{2}}}-R$.分析 同步卫星与地球自转同步,万有引力提供向心力,根据牛顿第二定律列式求解.
解答 解:同步卫星与地球自转同步,万有引力提供向心力,根据牛顿第二定律,有:
$G\frac{Mm}{{(R+h)}^{2}}=m\frac{4{π}^{2}(R+h)}{{T}^{2}}$
解得:$h=\root{3}{{\frac{{GM{T^2}}}{{4{π^2}}}}}-R$
故答案为:$\root{3}{\frac{GM{T}^{2}}{4{π}^{2}}}-R$
点评 本题关键明确同步卫星绕地球做匀速圆周运动(以太阳为参考系),根据万有引力提供向心力列式求解.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
17. 如图所示是一列简谐波在t=0时的波形图象,波速为v=10m/s,此时波恰传到I点,下列说法中正确的是( )
如图所示是一列简谐波在t=0时的波形图象,波速为v=10m/s,此时波恰传到I点,下列说法中正确的是( )
 如图所示是一列简谐波在t=0时的波形图象,波速为v=10m/s,此时波恰传到I点,下列说法中正确的是( )
如图所示是一列简谐波在t=0时的波形图象,波速为v=10m/s,此时波恰传到I点,下列说法中正确的是( )| A. | 此列波的周期为T=2.5s | |
| B. | 质点B、E在振动过程振幅相等 | |
| C. | 质点I的起振方向沿y轴正方向 | |
| D. | 当t=5.1s时,x=10m的质点处于平衡位置处 |
2.一物体在F1、F2…F6作用下做匀速直线运动,若突然撤去F2,其它力不变,则该物体( )
| A. | 可能做曲线运动 | B. | 一定做匀变速运动 | ||
| C. | 必沿F2反方向做直线运动 | D. | 必沿F2方向做直线运动 |
16.从离水平地面某一高度处,以大小不同的初速度水平抛出同一个小球,小球都落到该水平地面上.不计空气阻力.下列说法正确的是( )
| A. | 平抛初速度越大,小球在空中飞行时间越长 | |
| B. | 平抛初速度越大,小球落地时的末速度与水平地面的夹角越小 | |
| C. | 无论平抛初速度多大,小球落地时重力的功率都相等 | |
| D. | 以上说法都不对 |
 “嫦娥二号”卫星是在绕月极地轨道上运动的,加上月球的自转,卫星能探测到整个月球的表面.卫星CCD相机已对月球背面进行成像探测,并获取了月球背面部分区域的影像图.卫星在绕月极地轨道上做圆周运动时距月球表面高为H,绕行的周期为TM;月球绕地公转的周期为TE,半径为R0.地球半径为RE,月球半径为RM,忽略地球及太阳引力对绕月卫星的影响,月球与地球质量之比为($\frac{{T}_{E}}{{T}_{M}}$)2×($\frac{{R}_{M}+H}{{R}_{0}}$)3.
“嫦娥二号”卫星是在绕月极地轨道上运动的,加上月球的自转,卫星能探测到整个月球的表面.卫星CCD相机已对月球背面进行成像探测,并获取了月球背面部分区域的影像图.卫星在绕月极地轨道上做圆周运动时距月球表面高为H,绕行的周期为TM;月球绕地公转的周期为TE,半径为R0.地球半径为RE,月球半径为RM,忽略地球及太阳引力对绕月卫星的影响,月球与地球质量之比为($\frac{{T}_{E}}{{T}_{M}}$)2×($\frac{{R}_{M}+H}{{R}_{0}}$)3. 在“研究平抛物体的运动”实验中,某同学记录了A、B、C三点,取A点为坐标原点,建立了如图所示的坐标系.平抛轨迹上的这三点坐标值图中已标出,取g=10m/s2.那么小球平抛的初速度为1.5m/s,小球抛出点的坐标为(-30cm,-20cm)(坐标的单位用cm表示).
在“研究平抛物体的运动”实验中,某同学记录了A、B、C三点,取A点为坐标原点,建立了如图所示的坐标系.平抛轨迹上的这三点坐标值图中已标出,取g=10m/s2.那么小球平抛的初速度为1.5m/s,小球抛出点的坐标为(-30cm,-20cm)(坐标的单位用cm表示).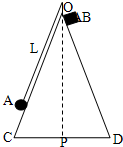 如图所示,有一个光滑的圆锥体固定在水平面上,在其顶点系一根长为L的细线,另一端拴一小物体A,使它刚好能贴着圆锥面做匀速圆周运动(即圆锥体对A无作用力),当运动到图中位置时,从圆锥的顶点O自由释放另一小物体B,使它沿着跟OC对称的另一条母线OD下滑.若圆锥体母线与轴线(OP)间夹角为θ,(设细线不干扰物体B的运动)求:
如图所示,有一个光滑的圆锥体固定在水平面上,在其顶点系一根长为L的细线,另一端拴一小物体A,使它刚好能贴着圆锥面做匀速圆周运动(即圆锥体对A无作用力),当运动到图中位置时,从圆锥的顶点O自由释放另一小物体B,使它沿着跟OC对称的另一条母线OD下滑.若圆锥体母线与轴线(OP)间夹角为θ,(设细线不干扰物体B的运动)求: