题目内容
18. “嫦娥二号”卫星是在绕月极地轨道上运动的,加上月球的自转,卫星能探测到整个月球的表面.卫星CCD相机已对月球背面进行成像探测,并获取了月球背面部分区域的影像图.卫星在绕月极地轨道上做圆周运动时距月球表面高为H,绕行的周期为TM;月球绕地公转的周期为TE,半径为R0.地球半径为RE,月球半径为RM,忽略地球及太阳引力对绕月卫星的影响,月球与地球质量之比为($\frac{{T}_{E}}{{T}_{M}}$)2×($\frac{{R}_{M}+H}{{R}_{0}}$)3.
“嫦娥二号”卫星是在绕月极地轨道上运动的,加上月球的自转,卫星能探测到整个月球的表面.卫星CCD相机已对月球背面进行成像探测,并获取了月球背面部分区域的影像图.卫星在绕月极地轨道上做圆周运动时距月球表面高为H,绕行的周期为TM;月球绕地公转的周期为TE,半径为R0.地球半径为RE,月球半径为RM,忽略地球及太阳引力对绕月卫星的影响,月球与地球质量之比为($\frac{{T}_{E}}{{T}_{M}}$)2×($\frac{{R}_{M}+H}{{R}_{0}}$)3.
分析 卫星绕月做圆周运动时,由月球的万有引力提供向心力,知道距月球表面高为H,月球半径为RM,绕行的周期为TM,根据由牛顿第二定律可求出月球的质量.月球绕地球公转时,由地球的万有引力提供向心力,由月球公转的周期为TE,半径为R0.地球半径为RE,根据由牛顿第二定律可求出地球的质量.
解答 解:由牛顿第二定律得:F向=man=m($\frac{2π}{T}$)2r;
万有引力定律公式为:F引=G$\frac{Mm}{{r}^{2}}$;
月球绕地公转时由万有引力提供向心力,故有:
G$\frac{{M}_{月}{M}_{地}}{{R}_{0}^{2}}$=M月($\frac{2π}{{T}_{E}}$)2R0…①
同理,探月卫星绕月运动时有:
G$\frac{{M}_{月}{M}_{卫}}{({R}_{M}+H)^{2}}$=M卫($\frac{2π}{{T}_{M}}$)2(RM+H)…②
由①②两式联立解得:
$\frac{{M}_{月}}{{M}_{地}}$=($\frac{{T}_{E}}{{T}_{M}}$)2×($\frac{{R}_{M}+H}{{R}_{0}}$)3
故答案为:($\frac{{T}_{E}}{{T}_{M}}$)2×($\frac{{R}_{M}+H}{{R}_{0}}$)3.
点评 本题是计算天体质量问题,利用万有引力与圆周运动知识的结合求解环绕天体的质量,是常用方法之一.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
9. a、b、c三个物体在同一条直线上运动,三个物体的位移-时间图象如图所示,图象c是一条抛物线,坐标原点是抛物线的顶点,下列说法中正确的是( )
a、b、c三个物体在同一条直线上运动,三个物体的位移-时间图象如图所示,图象c是一条抛物线,坐标原点是抛物线的顶点,下列说法中正确的是( )
 a、b、c三个物体在同一条直线上运动,三个物体的位移-时间图象如图所示,图象c是一条抛物线,坐标原点是抛物线的顶点,下列说法中正确的是( )
a、b、c三个物体在同一条直线上运动,三个物体的位移-时间图象如图所示,图象c是一条抛物线,坐标原点是抛物线的顶点,下列说法中正确的是( )| A. | a、b两物体都做匀速直线运动,两个物体的速度相同 | |
| B. | a、b两物体都做匀速直线运动,两个物体的速度大小相等方向相反 | |
| C. | 在0~5s的时间内,t=5s时,a、b两个物体相距最远 | |
| D. | 物体c做匀加速运动,加速度为0.2m/s2 |
13. 如图所示,粗糙的斜面体M放在粗糙的水平地面上,物块m恰好能在斜面体上沿斜面匀速下滑,斜面体保持静止不动,若用平行斜面向下的力F推动物块,使物块加速下滑,则斜面体( )
如图所示,粗糙的斜面体M放在粗糙的水平地面上,物块m恰好能在斜面体上沿斜面匀速下滑,斜面体保持静止不动,若用平行斜面向下的力F推动物块,使物块加速下滑,则斜面体( )
 如图所示,粗糙的斜面体M放在粗糙的水平地面上,物块m恰好能在斜面体上沿斜面匀速下滑,斜面体保持静止不动,若用平行斜面向下的力F推动物块,使物块加速下滑,则斜面体( )
如图所示,粗糙的斜面体M放在粗糙的水平地面上,物块m恰好能在斜面体上沿斜面匀速下滑,斜面体保持静止不动,若用平行斜面向下的力F推动物块,使物块加速下滑,则斜面体( )| A. | 受地面的摩擦力的大小为零 | |
| B. | 受地面的摩擦力的方向水平向右 | |
| C. | 受地面的摩擦力的方向水平向左 | |
| D. | 无论在多大的F作用下,斜面体都不可能沿水平地面运动 |
3.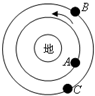 三颗人造卫星A、B、C在地球的大气层外沿如图所示的方向做匀速圆周运动,mA=mB<mC,则三颗卫星( )
三颗人造卫星A、B、C在地球的大气层外沿如图所示的方向做匀速圆周运动,mA=mB<mC,则三颗卫星( )
 三颗人造卫星A、B、C在地球的大气层外沿如图所示的方向做匀速圆周运动,mA=mB<mC,则三颗卫星( )
三颗人造卫星A、B、C在地球的大气层外沿如图所示的方向做匀速圆周运动,mA=mB<mC,则三颗卫星( )| A. | 线速度大小:vA>vB=vC | |
| B. | 周期:TA>TB=TC | |
| C. | 向心力大小:FA=FB<FC | |
| D. | 轨道半径和周期的关系:$\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}$=$\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}$=$\frac{{{R}_{C}}^{3}}{{{T}_{C}}^{2}}$ |
10.如图所示,木块A与水平圆盘保持相对静止,跟着圆盘一起做匀速圆周运动,则A所需的向心力是( )


| A. | 木块所受的重力 | B. | 圆盘对木块的支持力 | ||
| C. | 圆盘对木块的静摩擦力 | D. | 以上均不正确 |
8. 如图所示,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成θ角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊一小铁球,当小车向右做加速运动时,细线保持与竖直方向成α角,若θ<α,则下列说法正确的是( )
如图所示,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成θ角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊一小铁球,当小车向右做加速运动时,细线保持与竖直方向成α角,若θ<α,则下列说法正确的是( )
 如图所示,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成θ角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊一小铁球,当小车向右做加速运动时,细线保持与竖直方向成α角,若θ<α,则下列说法正确的是( )
如图所示,一小车上有一个固定的水平横杆,左边有一轻杆与竖直方向成θ角与横杆固定,下端连接一小铁球,横杆右边用一根细线吊一小铁球,当小车向右做加速运动时,细线保持与竖直方向成α角,若θ<α,则下列说法正确的是( )| A. | 轻杆对小球的弹力方向与细线平行 | |
| B. | 轻杆对小球的弹力方向沿着轻杆方向向上 | |
| C. | 轻杆对小球的弹力方向既不与细线平行,也不沿着轻杆方向 | |
| D. | 小车匀速时,θ=α |
 如图为一列简谐横波沿x轴正向传播时的波动图象.若x=4cm的质点振动周期为0.1s,则:它此时的振动方向为向上,波速为0.8m/s.
如图为一列简谐横波沿x轴正向传播时的波动图象.若x=4cm的质点振动周期为0.1s,则:它此时的振动方向为向上,波速为0.8m/s.