��Ŀ����
12��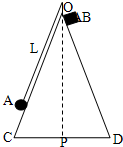 ��ͼ��ʾ����һ���⻬��Բ��̶���ˮƽ���ϣ����䶥��ϵһ����ΪL��ϸ�ߣ���һ��˩һС����A��ʹ���պ�������Բ��������Բ���˶�����Բ���A���������������˶���ͼ��λ��ʱ����Բ�Ķ���O�����ͷ���һС����B��ʹ�����Ÿ�OC�ԳƵ���һ��ĸ��OD�»�����Բ��ĸ�������ߣ�OP����н�Ϊ�ȣ�����ϸ�߲���������B���˶�����
��ͼ��ʾ����һ���⻬��Բ��̶���ˮƽ���ϣ����䶥��ϵһ����ΪL��ϸ�ߣ���һ��˩һС����A��ʹ���պ�������Բ��������Բ���˶�����Բ���A���������������˶���ͼ��λ��ʱ����Բ�Ķ���O�����ͷ���һС����B��ʹ�����Ÿ�OC�ԳƵ���һ��ĸ��OD�»�����Բ��ĸ�������ߣ�OP����н�Ϊ�ȣ�����ϸ�߲���������B���˶�������1������A�˶��Ľ��ٶȴ�С
��2������B��ĸ���»�L��������ʱ��
��3��Ҫʹ����A�ܹ�������B������Բ��ĸ�������ߣ�OP����нǦ�ӦΪ����������Ǻ�����ʾ��
���� ��1���������������������ݾ���ĺ����ṩ��������ͨ��ţ�ٵڶ������������A�˶��Ľ��ٶȴ�С��
��2������ţ�ٵڶ������������B�ļ��ٶȣ�����λ��ʱ�乫ʽ�������B���˶�ʱ�䣮
��3��Ҫʹ����A�ܹ�������B������B���˶�ʱ����ڰ��A�����ڵ���������
��� �⣺��1����A�պ�������Բ������Բ���˶�������A������ͼ��ʾ��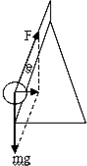
��mgtan��=mLsin�Ȧ�2��
���$��=\sqrt{\frac{g}{Lcos��}}$��
��2������B��ĸ���������ȼ���ֱ���˶������ٶ�a=gcos��
��$\frac{1}{2}gcos��{t}^{2}=L$
���t=$\sqrt{\frac{2L}{gcos��}}$��
��3��Ҫʹ������������������t=$��n+\frac{1}{2}��\frac{2��}{��}$����n=0��1��2��3����
��$\sqrt{\frac{2L}{gcos��}}=��n+\frac{1}{2}��\frac{2��}{��}$��
���cos��=$\frac{L{��}^{2}}{2{��}^{2}g��n+\frac{1}{2}��^{2}}$����n=0��1��2��3����
�𣺣�1������A�˶��Ľ��ٶȴ�СΪ$\sqrt{\frac{g}{Lcos��}}$��
��2������B��ĸ���»�L��������ʱ��Ϊ$\sqrt{\frac{2L}{gcos��}}$��
��3��Ҫʹ����A�ܹ�������B������Բ��ĸ�������ߣ�OP����нǦȵ�����Ϊ$\frac{L{��}^{2}}{2{��}^{2}g��n+\frac{1}{2}��^{2}}$����n=0��1��2��3������
���� �������Ĺؼ�֪��Բ���˶�����������Դ�����ţ�ٵڶ����ɽ�����⣬ע��Բ���˶��������ԣ�

 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�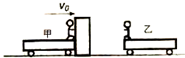 ��ͼ��ʾ���ס�����С������һ��������ˮƽ���������棬�����ı���������Ϊ30kg���Һ����ı���������Ϊ30kg����Ϸʱ������һ����Ϊ10kg��ľ�䣬����һ����v0=3.5m/s���ٶȻ��У����ڼ���ǰ����Ե��澲ֹ��Ϊ������ײ�������������Ե�������ٶȽ������Ƴ����ܱ���������ײ����������
��ͼ��ʾ���ס�����С������һ��������ˮƽ���������棬�����ı���������Ϊ30kg���Һ����ı���������Ϊ30kg����Ϸʱ������һ����Ϊ10kg��ľ�䣬����һ����v0=3.5m/s���ٶȻ��У����ڼ���ǰ����Ե��澲ֹ��Ϊ������ײ�������������Ե�������ٶȽ������Ƴ����ܱ���������ײ����������| A�� | 8m/s | B�� | 3 m/s | C�� | 6 m/s | D�� | 10 m/s |
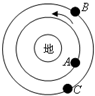 ������������A��B��C�ڵ���Ĵ�����������ͼ��ʾ�ķ���������Բ���˶���mA=mB��mC�����������ǣ�������
������������A��B��C�ڵ���Ĵ�����������ͼ��ʾ�ķ���������Բ���˶���mA=mB��mC�����������ǣ�������| A�� | ���ٶȴ�С��vA��vB=vC | |
| B�� | ���ڣ�TA��TB=TC | |
| C�� | ����������FA=FB��FC | |
| D�� | ����뾶�����ڵĹ�ϵ��$\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}$=$\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}$=$\frac{{{R}_{C}}^{3}}{{{T}_{C}}^{2}}$ |
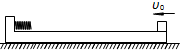 ��ͼ��ʾ��һ������ΪM��ľ��ͣ�ڹ⻬��ˮƽ���ϣ�ľ�������е��壬�����Ϲ̶�һ��С���ɣ�һ������Ϊm��С��飨����Ϊ�ʵ㣩��ˮƽ�ٶȦ�0��ľ����Ҷ˿�ʼ�����˶����뵯����ײ���ɴ��ڵ������ڣ���������ǡ��ͣ��ľ����Ҷˣ����������龰����֪�������������������
��ͼ��ʾ��һ������ΪM��ľ��ͣ�ڹ⻬��ˮƽ���ϣ�ľ�������е��壬�����Ϲ̶�һ��С���ɣ�һ������Ϊm��С��飨����Ϊ�ʵ㣩��ˮƽ�ٶȦ�0��ľ����Ҷ˿�ʼ�����˶����뵯����ײ���ɴ��ڵ������ڣ���������ǡ��ͣ��ľ����Ҷˣ����������龰����֪�������������������| A�� | ���ɵľ���ϵ�� | |
| B�� | ���ɵ���������� | |
| C�� | ľ���С�����ɵ�ϵͳ������ʧ�Ļ�е�� | |
| D�� | ������֪ľ�峤��l�������ľ���С����Ķ�Ħ������ |
 ��ͼ��ʾ����һ������Ϊ2�ȣ���=53�㣩�ĵ����Ĺ⻬Բ���ڣ���������Ϊm=1kg��С���壬С��������ֱת��OO��֮������Բĸ��ƽ�С���ΪL=1m������ϸ����������ʹϸ�߲��ɳڣ�С������Բ��һ��������Բ���˶��Ľ��ٶȦؿ���Ϊ����������gȡ10m/s2��sin53��=0.8��
��ͼ��ʾ����һ������Ϊ2�ȣ���=53�㣩�ĵ����Ĺ⻬Բ���ڣ���������Ϊm=1kg��С���壬С��������ֱת��OO��֮������Բĸ��ƽ�С���ΪL=1m������ϸ����������ʹϸ�߲��ɳڣ�С������Բ��һ��������Բ���˶��Ľ��ٶȦؿ���Ϊ����������gȡ10m/s2��sin53��=0.8��| A�� | 2rad/s | B�� | 3rad/s | C�� | 4rad/s | D�� | 5rad/s |
 ��ͼ��ʾ����ˮƽ������������ֱ���˶���С����ͨ�������������ӵ���һ�����壬��С���ͱ�����������ͬһʱ�̵��ٶȷֱ�Ϊv1��v2�����Ӷ����������ΪFT��������������ΪG��������˵����ȷ���ǣ�������
��ͼ��ʾ����ˮƽ������������ֱ���˶���С����ͨ�������������ӵ���һ�����壬��С���ͱ�����������ͬһʱ�̵��ٶȷֱ�Ϊv1��v2�����Ӷ����������ΪFT��������������ΪG��������˵����ȷ���ǣ�������| A�� | �����������˶�����v1=v2 | B�� | �����������˶�����v2��v1 | ||
| C�� | �����������˶�����FT��G | D�� | �����������˶�����FT=G |
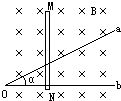 ��ͼ��ʾ���������aOb�ļн�Ϊ����ˮƽ��������ֱ���µ���ǿ�ų��У��ų��ĴŸ�Ӧǿ��ΪB��������MNʼ�����ܽӴ����ã�������Ob�ߴ�ֱ����t=0ʱ��������O�㿪ʼ���ٶ�v�����˶�������tʱ�̱պϵ�·�ڸ�Ӧ�綯�ƵĴ�СΪBv2t tan����
��ͼ��ʾ���������aOb�ļн�Ϊ����ˮƽ��������ֱ���µ���ǿ�ų��У��ų��ĴŸ�Ӧǿ��ΪB��������MNʼ�����ܽӴ����ã�������Ob�ߴ�ֱ����t=0ʱ��������O�㿪ʼ���ٶ�v�����˶�������tʱ�̱պϵ�·�ڸ�Ӧ�綯�ƵĴ�СΪBv2t tan����