题目内容
15．
在“研究平抛物体的运动”实验中，某同学记录了A、B、C三点，取A点为坐标原点，建立了如图所示的坐标系．平抛轨迹上的这三点坐标值图中已标出，取g=10m/s2．那么小球平抛的初速度为1.5m/s，小球抛出点的坐标为（-30cm，-20cm）（坐标的单位用cm表示）．
分析 抛运动在水平方向做匀速直线运动，在竖直方向做自由落体运动．根据竖直方向上△y=gT2，求出时间间隔，然后根据水平方向上的匀速直线运动求出初速度．求出B点在竖直方向上的速度，即可求出运动到B点的时间，从而求出运动的水平位移和竖直位移，即可求出平抛运动的初始位置．
解答 解：在竖直方向上△y=gT2，则：T=$\sqrt{\frac{△y}{g}}$=$\sqrt{\frac{（1.6-0.6）-0.6}{10}}$s=0.2s．
则初速度：v=$\frac{x}{T}$=$\frac{0.3}{0.2}$m/s=1.5m/s
B点竖直方向上的分速度为：vBy=$\frac{{y}_{AC}}{2T}$=$\frac{1.6}{0.4}$ m/s=4m/s
则运动到B点的时间：t=$\frac{{v}_{By}}{g}$=0.4s
小球从抛出点到A点的时间为：
△t=t-T=0.4s-0.2s=0.2s
因此抛出点到A点的水平、竖直距离故答案为：
x=v0△t=1.5m/s×0.2s=0.3m=30cm
y=$\frac{1}{2}$gt2=$\frac{1}{2}$×10m×（0.2）2=0.2m=20cm
因此抛出点的坐标为：（-30cm，-20cm）．
故答案为：1.5，（-30cm，-20cm）．
点评 解决本题的关键掌握平抛运动在水平方向做匀速直线运动，在竖直方向上做自由落体运动．
练习册系列答案
相关题目
相距为d的两平行金属板M、N与电池相连接，如图所示，一带电粒子从M板左边缘垂直于电场方向射入，并打到N板的中心．现欲使粒子原样射入，能从极板间射出电场，在下列两种情况下，分别求出N板向下移动的距离x取值范围（不计重力）． 
3．
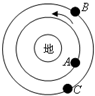三颗人造卫星A、B、C在地球的大气层外沿如图所示的方向做匀速圆周运动，mA=mB＜mC，则三颗卫星（ ）
三颗人造卫星A、B、C在地球的大气层外沿如图所示的方向做匀速圆周运动，mA=mB＜mC，则三颗卫星（ ）| A． | 线速度大小：vA＞vB=vC | |
| B． | 周期：TA＞TB=TC | |
| C． | 向心力大小：FA=FB＜FC | |
| D． | 轨道半径和周期的关系：$\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}$=$\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}$=$\frac{{{R}_{C}}^{3}}{{{T}_{C}}^{2}}$ |
10．如图所示，木块A与水平圆盘保持相对静止，跟着圆盘一起做匀速圆周运动，则A所需的向心力是（ ）
| A． | 木块所受的重力 | B． | 圆盘对木块的支持力 | ||
| C． | 圆盘对木块的静摩擦力 | D． | 以上均不正确 |
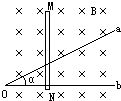如图所示，金属框架aOb的夹角为α，水平放置在竖直向下的匀强磁场中，磁场的磁感应强度为B．金属棒MN始终与框架接触良好，且与框架Ob边垂直．在t=0时金属棒自O点开始以速度v向右运动，则在t时刻闭合电路内感应电动势的大小为Bv2t tanα．