题目内容
14.在“验证机械能守恒定律”的一次实验中,如图甲所示,质量m=1kg的重物自由下落,在纸带上打出一系列的点,图乙中O点为打出的起始点,且速度为零.(其中一段纸带图中未画出)选取在纸带上连续打出的点A、B、C、D、E、F、G作为计数点.其中测出D、E、F点距起始点O的距离如图所示.已知打点计时器打点周期为T=0.02s.(g取10m/s2)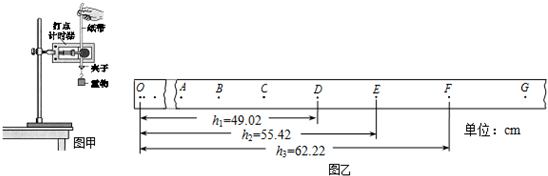
(1)图乙中纸带的左端与重物相连(填左或右);
(2)打点计时器打下计数点E时,物体的速度vE=3.3 m/s;
(3)从起点0到打下计数点E的过程中物体的重力势能减少量△EP=5.54 J(结果保留3位有效数字),此过程中物体动能的增加量△EK=5.45 J (结果保留3位有效数字).
(4)实验的结论是在误差允许范围内,重物的机械能守恒.
分析 根据相等时间内的位移越来越大,确定哪一端与重物相连;
纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度,从而求出动能.再根据功能关系得重力势能减小量等于重力做功的数值.
依据误差允许范围内,即可判定重物的机械能是否守恒.
解答 解:(1)从纸带数据可以看出,相等时间内的位移越来越大,则纸带的左端与重物相连.
(2)利用匀变速直线运动的推论有:
vE=$\frac{{x}_{DF}}{2T}$=$\frac{0.6222-0.4902}{2×0.02}$=3.3m/s
(3)从打点计时器打下起点O到打下C点的过程中,重力势能减小量为:
△Ep=mgh=1×9.8×0.5542J≈5.54J.
EkB=$\frac{1}{2}$mvB2=$\frac{1}{2}$×1×3.32≈5.45 J,
(4)由于重力势能减小量略大于动能的增加量,在误差允许范围内,重物下落的机械能守恒.
故答案为:(1)左;(2)3.3;(3)5.54,5.45;(4 )在误差允许范围内,重物下落的机械能守恒.
点评 要知道重物带动纸带下落过程中能量转化的过程和能量守恒.
重物带动纸带下落过程中,除了重力还受到阻力,从能量转化的角度,由于阻力做功,重力势能减小除了转化给了动能还有一部分转化给摩擦产生的内能.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
2.质量为m的人造地球卫星,在半径为r的圆轨道上绕地球运行时,其线速度为v,角速度为ω,取地球质量为M,当这颗人造地球卫星的轨道半径为2r的圆轨道上绕地球运行时,则( )
| A. | 根据公式v=$\sqrt{\frac{GM}{r}}$,可知卫星运动的线速度将减小到$\frac{v}{\sqrt{2}}$ | |
| B. | 根据公式F=m$\frac{{v}^{2}}{r}$,可知卫星所需的向心力将减小到原来的$\frac{1}{2}$ | |
| C. | 根据公式ω=$\frac{v}{r}$,可知卫星的角速度将减小到$\frac{ω}{2}$ | |
| D. | 根据F=G$\frac{Mm}{{r}^{2}}$,可知卫星的向心力减小为原来的$\frac{1}{4}$ |
9. 我国自行研制的新一代ZBL-09 8×8轮式步兵装甲车已达到国际领先水平,已成为中国军方快速部署型轻装甲部队的主力装备.该装甲车在平直的公路上从静止开始加速,经过较短的时间t和距离s速度便可达到最大值vm.设在加速过程中发动机的功率恒定为P,装甲车所受阻力恒为f,以下说法不正确的是( )
我国自行研制的新一代ZBL-09 8×8轮式步兵装甲车已达到国际领先水平,已成为中国军方快速部署型轻装甲部队的主力装备.该装甲车在平直的公路上从静止开始加速,经过较短的时间t和距离s速度便可达到最大值vm.设在加速过程中发动机的功率恒定为P,装甲车所受阻力恒为f,以下说法不正确的是( )
 我国自行研制的新一代ZBL-09 8×8轮式步兵装甲车已达到国际领先水平,已成为中国军方快速部署型轻装甲部队的主力装备.该装甲车在平直的公路上从静止开始加速,经过较短的时间t和距离s速度便可达到最大值vm.设在加速过程中发动机的功率恒定为P,装甲车所受阻力恒为f,以下说法不正确的是( )
我国自行研制的新一代ZBL-09 8×8轮式步兵装甲车已达到国际领先水平,已成为中国军方快速部署型轻装甲部队的主力装备.该装甲车在平直的公路上从静止开始加速,经过较短的时间t和距离s速度便可达到最大值vm.设在加速过程中发动机的功率恒定为P,装甲车所受阻力恒为f,以下说法不正确的是( )| A. | 装甲车加速过程中,牵引力对它做功为Pt | |
| B. | 装甲车的最大速度vm=$\frac{P}{f}$ | |
| C. | 装甲车加速过程中,装甲车做加速度变小的加速直线运动 | |
| D. | 装甲车的质量 m=$\frac{2Pt}{{{v}_{m}}^{2}}$ |
19.某物体在x轴上做直线运动,在0~8s内的位移-时间图象如图所示,则下列说法正确的是( )


| A. | 物体在0~8s时间内的位移方向沿x轴负方向 | |
| B. | 物体在0~2s时间内做匀减速运动 | |
| C. | 物体在2s~4s时间内发生的位移是12m | |
| D. | 物体在t=1s时刻的速度大于t=6s时刻的速度 |
6.如图所示,高度相同、底边等长的光滑斜面和光滑曲面固定在水平地面上,两个完全相同的小球A和B分别从两个面的顶端由静止滑向底端,则( )


| A. | 到达底端时两球的动能相等 | B. | 到达底端时两球重力的功率相等 | ||
| C. | 下滑过程两球重力所做的功不等 | D. | 下滑不同高度时两球的机械能相等 |
15.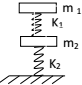 如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧.在这过程中上面木块移动的距离为( )
如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧.在这过程中上面木块移动的距离为( )
 如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧.在这过程中上面木块移动的距离为( )
如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧.在这过程中上面木块移动的距离为( )| A. | $\frac{{m}_{1}g}{{k}_{1}}$ | B. | $\frac{{m}_{1}g}{{k}_{1}}$+$\frac{{m}_{2}g}{{k}_{2}}$ | C. | $\frac{{m}_{1}g}{{k}_{1}}$+$\frac{{m}_{1}g}{{k}_{2}}$ | D. | $\frac{{(m}_{1}{+m}_{2})g}{{k}_{1}}$ |
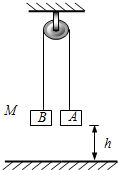 如图所示,一根细绳绕过光滑的定滑轮,两端分别系住A、B两物体,其质量M都为2kg,使A、B静止于同一高度,离地高度h为1m,现轻轻的放一质量为1kg的小物体C到A上且粘连,重力加速度g取10m/s2,设绳足够长,绳与滑轮的质量不计,A、B、C都可视为质点.
如图所示,一根细绳绕过光滑的定滑轮,两端分别系住A、B两物体,其质量M都为2kg,使A、B静止于同一高度,离地高度h为1m,现轻轻的放一质量为1kg的小物体C到A上且粘连,重力加速度g取10m/s2,设绳足够长,绳与滑轮的质量不计,A、B、C都可视为质点.