题目内容
15.宇航员将一小球从某星球表面上方h高处由静止释放,小球经时间t落到星球表面.已知该星球的半径为R,且h<<R,引力常量为G,小球下落时的阻力不计.求:(1)该星球表面的重力加速度g的大小;
(2)该星球的质量M;
(3)该星球的第一宇宙速度v的大小.
分析 (1)根据自由落体的位移时间规律可以直接求出星球表面的重力加速度;
(2)根据星球表面重力和万有引力相等,利用求出的重力加速度和星球半径可以求出星球的质量M;
(3)飞行器靠近星球表面飞行时,飞行器所受星球万有引力提供星球的向心力,从而求出“第一宇宙速度”大小.
解答 解:(1)小球下落的过程中有:h=$\frac{1}{2}g{t}^{2}$;
解得:g=$\frac{2h}{{t}^{2}}$;
(2)设物体质量为m,星球对它的引力等于其重力,有:
mg=G$\frac{Mm}{{R}^{2}}$
解得星球质量:
M=$\frac{2h{R}^{2}}{G{t}^{2}}$
(3)由牛顿第二定律得:mg=m$\frac{{v}^{2}}{R}$;
解得该星球的第一宇宙速度:v=$\frac{\sqrt{2hR}}{t}$;
答:(1)该星球表面的重力加速度g的大小为$\frac{2h}{{t}^{2}}$;
(2)该星球的质量M为$\frac{2h{R}^{2}}{G{t}^{2}}$;
(3)该星球的第一宇宙速度v的大小为$\frac{\sqrt{2hR}}{t}$.
点评 结合自由落体运动规律求月球表面的重力加速度,根据万有引力与重力相等和万有引力提供圆周运动向心力求解中心天体质量和近月飞行的速度v.

练习册系列答案
相关题目
4.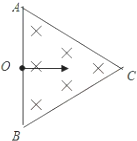 如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
 如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )
如图所示,由光滑弹性绝缘壁构成的等边三角形ABC容器的边长为a,其内存在垂直纸面向外的匀强磁场,小孔O是竖直边AB的中点,一质量为为m、电荷量为+q的粒子(不计重力)从小孔O以速度v水平射入磁场,粒子与器壁多次垂直碰撞后(碰撞时无能量和电荷量损失)仍能从O孔水平射出,已知粒子在磁场中运行的半径小于$\frac{a}{2}$,则磁场的磁感应强度的最小值Bmin及对应粒子在磁场中运行的时间t为( )| A. | Bmin=$\frac{2m{v}_{0}}{qa}$,t=$\frac{7πa}{6v}$ | B. | Bmin=$\frac{2m{v}_{0}}{qa}$,t=$\frac{πa}{26v}$ | ||
| C. | Bmin=$\frac{6m{v}_{0}}{qa}$,t=$\frac{7πa}{6v}$ | D. | Bmin=$\frac{6m{v}_{0}}{qa}$,t=$\frac{πa}{26v}$ |
6. 如图所示,虚线表示某电场中的四个等势面,相邻等势面间的电势差相等,一不计重力的带负电的粒子从右侧垂直等势面φ4向左进入电场,运动轨迹与等势面分别交于a,b,c三点,则可以判断( )
如图所示,虚线表示某电场中的四个等势面,相邻等势面间的电势差相等,一不计重力的带负电的粒子从右侧垂直等势面φ4向左进入电场,运动轨迹与等势面分别交于a,b,c三点,则可以判断( )
 如图所示,虚线表示某电场中的四个等势面,相邻等势面间的电势差相等,一不计重力的带负电的粒子从右侧垂直等势面φ4向左进入电场,运动轨迹与等势面分别交于a,b,c三点,则可以判断( )
如图所示,虚线表示某电场中的四个等势面,相邻等势面间的电势差相等,一不计重力的带负电的粒子从右侧垂直等势面φ4向左进入电场,运动轨迹与等势面分别交于a,b,c三点,则可以判断( )| A. | φ1<φ2<φ3<φ4 | |
| B. | 粒子的运动轨迹和φ3等势面也可能垂直 | |
| C. | φ4等势面上各点场强处处相等 | |
| D. | 该区域可能是点电荷和无限大金属平板形成的电场 |
3. 如图所示,弹簧振子在A、B间做简谐运动,O为平衡位置,A、B间的距离是20cm,振子由A运动到B的时间是2s,则( )
如图所示,弹簧振子在A、B间做简谐运动,O为平衡位置,A、B间的距离是20cm,振子由A运动到B的时间是2s,则( )
 如图所示,弹簧振子在A、B间做简谐运动,O为平衡位置,A、B间的距离是20cm,振子由A运动到B的时间是2s,则( )
如图所示,弹簧振子在A、B间做简谐运动,O为平衡位置,A、B间的距离是20cm,振子由A运动到B的时间是2s,则( )| A. | 从O→B→O振子做了一次全振动 | |
| B. | 振动周期为2 s,振幅是10 cm | |
| C. | 从B开始经过6 s,振子通过的路程是60 cm | |
| D. | 振子在经过C点时速度大小一定相等,加速度也一定相等 | |
| E. | 从O开始经过3 s,振子的弹性势能最大 |
10. 弹簧振子以O点为平衡位置在B、C两点之间做简谐运动,B、C相距20 cm.某时刻振子处于B点,经过0.5 s,振子首次到达C点.下列说法中正确的是( )
弹簧振子以O点为平衡位置在B、C两点之间做简谐运动,B、C相距20 cm.某时刻振子处于B点,经过0.5 s,振子首次到达C点.下列说法中正确的是( )
 弹簧振子以O点为平衡位置在B、C两点之间做简谐运动,B、C相距20 cm.某时刻振子处于B点,经过0.5 s,振子首次到达C点.下列说法中正确的是( )
弹簧振子以O点为平衡位置在B、C两点之间做简谐运动,B、C相距20 cm.某时刻振子处于B点,经过0.5 s,振子首次到达C点.下列说法中正确的是( )| A. | 该弹簧振子的振幅为20cm | |
| B. | 该弹簧振子的周期为1s | |
| C. | 该弹簧振子的频率为2Hz | |
| D. | 振子从O点出发到再次回到O点的过程是一次全振动 |
5.飞船围绕太阳在近似圆周的轨道上运动,若其轨道半径是地球轨道半径的9倍,则宇宙飞船绕太阳运行的周期是( )
| A. | 3年 | B. | 9年 | C. | 27年 | D. | 81年 |
 竖直平面内有一直角形内径相同的细玻璃管,A端封闭,C端开口,最初AB段处于水平状态,中间有一段水银将气体封闭在A端,各部分尺寸如图所示,外界大气压强p0=75cmHg.
竖直平面内有一直角形内径相同的细玻璃管,A端封闭,C端开口,最初AB段处于水平状态,中间有一段水银将气体封闭在A端,各部分尺寸如图所示,外界大气压强p0=75cmHg. 如图为某小球做平抛运动时,用闪光照相的方法获得的相片的一部分,图中背景方格的边长为5cm,g=10m/s2,则
如图为某小球做平抛运动时,用闪光照相的方法获得的相片的一部分,图中背景方格的边长为5cm,g=10m/s2,则