题目内容
1. 如图所示,质量为m=2kg的木块在倾角θ=37°的斜面上由静止开始下滑(斜面足够长),木块在斜面上所受的摩擦力为8N(sin37°=0.6,cos37°=0.8)求:
如图所示,质量为m=2kg的木块在倾角θ=37°的斜面上由静止开始下滑(斜面足够长),木块在斜面上所受的摩擦力为8N(sin37°=0.6,cos37°=0.8)求:(1)前2s内下滑的距离;
(2)前2s内重力做的功;
(3)第2s末重力的瞬时功率.
分析 (1)通过受力分析求出物体下滑时的加速度,由运动学公式求出2s内下滑的位移;
(2)由功的定义求出重力做的功;
(3)求出2s末的速度,由P=Fv求出瞬时功率;
解答 解:(1)由F合=ma得,木块的加速度:a=$\frac{{F}_{合}}{m}$=$\frac{mgsin3{7}^{0}-f}{m}$=gsin37°-$\frac{f}{m}$=2m/s2
前2s内木块的位移:s=$\frac{1}{2}$at2=$\frac{1}{2}$×2×22m=4m
(2)重力在前2s内做的功:W=mgsinθ•S=2×10×0.6×4J=48J
(3)木块在第2s末的瞬时速度为:v=at=2×2m/s=4m/s
第2s末重力的瞬时功率为:P=mgsinθ•v=2×10×0.6×4W=48W
答:(1)前2s内下滑的距离为4m;
(2)求2s内重力做的功为48J;
(3)第2s末重力的瞬时功率48W.
点评 本题考查了牛顿第二定律和运动学公式与功与功率的综合运用,知道加速度是联系力学和运动学的桥梁.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
11. 如图所示,从地面上的A点以速度v竖直向上抛出一小球,上升至最高点B后返回,O为A、B的中点,小球在运动过程中受到的空气阻力大小不变.下列说法正确的是( )
如图所示,从地面上的A点以速度v竖直向上抛出一小球,上升至最高点B后返回,O为A、B的中点,小球在运动过程中受到的空气阻力大小不变.下列说法正确的是( )
 如图所示,从地面上的A点以速度v竖直向上抛出一小球,上升至最高点B后返回,O为A、B的中点,小球在运动过程中受到的空气阻力大小不变.下列说法正确的是( )
如图所示,从地面上的A点以速度v竖直向上抛出一小球,上升至最高点B后返回,O为A、B的中点,小球在运动过程中受到的空气阻力大小不变.下列说法正确的是( )| A. | 小球上升至O点时的速度等于0.5v | |
| B. | 小球上升至O点时的速度小于0.5v | |
| C. | 小球在上升过程中重力的冲量小于下降过程中重力的冲量 | |
| D. | 小球在上升过程中动能的减少量等于下降过程中动能的增加量 |
12.在物理学的发展过程中,科学的物理思想与方法对物理学的发展起到了重要作用,下列关于物理思想和方法说法正确的是( )
| A. | 质点和点电荷是同一种思想方法 | |
| B. | 重心、合力都体现了等效思想 | |
| C. | 伽利略用小球在斜面上的运动验证了速度与位移成正比 | |
| D. | 牛顿第一定律是利用逻辑思维对事实进行分析的产物,不可能用实验直接证明 |
16. 如图所示,质量为m的小物块从A处由静止开始沿倾角为θ的光滑斜面AO下滑,进入粗糙水平面继续滑动,最终停在B处.已知A距水平面OB的高度为物块与水平面间的动摩擦因数恒为μ,重力加速度大小为g.则( )
如图所示,质量为m的小物块从A处由静止开始沿倾角为θ的光滑斜面AO下滑,进入粗糙水平面继续滑动,最终停在B处.已知A距水平面OB的高度为物块与水平面间的动摩擦因数恒为μ,重力加速度大小为g.则( )
 如图所示,质量为m的小物块从A处由静止开始沿倾角为θ的光滑斜面AO下滑,进入粗糙水平面继续滑动,最终停在B处.已知A距水平面OB的高度为物块与水平面间的动摩擦因数恒为μ,重力加速度大小为g.则( )
如图所示,质量为m的小物块从A处由静止开始沿倾角为θ的光滑斜面AO下滑,进入粗糙水平面继续滑动,最终停在B处.已知A距水平面OB的高度为物块与水平面间的动摩擦因数恒为μ,重力加速度大小为g.则( )| A. | O、B两点间的距离为$\frac{h}{μ}$ | |
| B. | O、B两点间的距离为μh | |
| C. | 物块滑到斜面底端时重力的功率为mg$\sqrt{2gh}$ | |
| D. | 物块滑到斜面底端时重力的功率为mg$\sqrt{2gh}$cosθ |
10. 电子只在电场力作用下由a点运动到b点的轨迹如图中虚线所示,图中一组平行且距离相等的实线可能是电场线,也可能是等势面,以下判断中正确的是( )
电子只在电场力作用下由a点运动到b点的轨迹如图中虚线所示,图中一组平行且距离相等的实线可能是电场线,也可能是等势面,以下判断中正确的是( )
 电子只在电场力作用下由a点运动到b点的轨迹如图中虚线所示,图中一组平行且距离相等的实线可能是电场线,也可能是等势面,以下判断中正确的是( )
电子只在电场力作用下由a点运动到b点的轨迹如图中虚线所示,图中一组平行且距离相等的实线可能是电场线,也可能是等势面,以下判断中正确的是( )| A. | 无论图中实线是电场线还是等势面,a点的电势都比b点低 | |
| B. | 无论图中实线是电场线还是等势面,a点的电场强度都比b点小 | |
| C. | 如果图中实线是等势面,电子在a点动能较在b点小 | |
| D. | 如果图中实线是电场线,电子在a点动能较在b点小 |
11.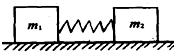 如图所示,将木块m1和m2放在被压缩的轻质弹簧两端,并用细棉丝固定,当用火焰将棉丝烧断时,在弹簧作用下两木块被弹开.已知m2=$\frac{1}{2}$m1,并假定两木块始终受到相等的恒定阻力,它们与弹簧脱离后,沿水平方向分别运动距离s1和s2即停止,则( )
如图所示,将木块m1和m2放在被压缩的轻质弹簧两端,并用细棉丝固定,当用火焰将棉丝烧断时,在弹簧作用下两木块被弹开.已知m2=$\frac{1}{2}$m1,并假定两木块始终受到相等的恒定阻力,它们与弹簧脱离后,沿水平方向分别运动距离s1和s2即停止,则( )
 如图所示,将木块m1和m2放在被压缩的轻质弹簧两端,并用细棉丝固定,当用火焰将棉丝烧断时,在弹簧作用下两木块被弹开.已知m2=$\frac{1}{2}$m1,并假定两木块始终受到相等的恒定阻力,它们与弹簧脱离后,沿水平方向分别运动距离s1和s2即停止,则( )
如图所示,将木块m1和m2放在被压缩的轻质弹簧两端,并用细棉丝固定,当用火焰将棉丝烧断时,在弹簧作用下两木块被弹开.已知m2=$\frac{1}{2}$m1,并假定两木块始终受到相等的恒定阻力,它们与弹簧脱离后,沿水平方向分别运动距离s1和s2即停止,则( )| A. | s1=4s2 | B. | s1=s2 | C. | s1=$\frac{1}{2}$s2 | D. | s1=2s2 |
 如图所示,半径R=0.8m的竖直光滑四分之一圆弧轨道固定在水平面上,质量为m=0.4kg的滑块从圆弧轨道的最高点由静止释放,当滑块运动到圆弧轨道的最低点A时,装在滑块内部的微量炸药发生爆炸,将滑块炸成拨质量之比为$\frac{{m}_{1}}{{m}_{2}}$=$\frac{1}{3}$的两块P、Q,其中P刚好又能回到圆弧轨道的最高点,Q沿水平面向右滑行.已知Q与水平面间的动摩擦因数为μ=$\frac{2}{3}$,炸药的质量忽略不计,重力加速度g=10m/s2.
如图所示,半径R=0.8m的竖直光滑四分之一圆弧轨道固定在水平面上,质量为m=0.4kg的滑块从圆弧轨道的最高点由静止释放,当滑块运动到圆弧轨道的最低点A时,装在滑块内部的微量炸药发生爆炸,将滑块炸成拨质量之比为$\frac{{m}_{1}}{{m}_{2}}$=$\frac{1}{3}$的两块P、Q,其中P刚好又能回到圆弧轨道的最高点,Q沿水平面向右滑行.已知Q与水平面间的动摩擦因数为μ=$\frac{2}{3}$,炸药的质量忽略不计,重力加速度g=10m/s2. 如图所示,一质量m=2000kg的汽车在平直公路上以v1=20m/s的速度向前匀速行驶,汽车发动机的输出功率P=30kw保持不变.现在两只汽车后轮的轮胎被抛散在路面上的废铁扎破而突然泄气,导致汽车行驶的阻力增大,但驾驶员没有及时察觉,依然保持原来的输出功率行驶,20s后发现问题立即关闭汽车发动机,此时汽车已经以v2=15m/s速度匀速行驶一段距离.假设汽车在轮胎扎破到最后停下的过程中所受阻力始终恒定.
如图所示,一质量m=2000kg的汽车在平直公路上以v1=20m/s的速度向前匀速行驶,汽车发动机的输出功率P=30kw保持不变.现在两只汽车后轮的轮胎被抛散在路面上的废铁扎破而突然泄气,导致汽车行驶的阻力增大,但驾驶员没有及时察觉,依然保持原来的输出功率行驶,20s后发现问题立即关闭汽车发动机,此时汽车已经以v2=15m/s速度匀速行驶一段距离.假设汽车在轮胎扎破到最后停下的过程中所受阻力始终恒定. 如图,质量为m的物体在粗糙斜面上以加速度a加速下滑,(1)现加一个恒力F作用在物体上,力F过物体的重心,且方向竖直向下,则之后物体的加速度将A.
如图,质量为m的物体在粗糙斜面上以加速度a加速下滑,(1)现加一个恒力F作用在物体上,力F过物体的重心,且方向竖直向下,则之后物体的加速度将A.