题目内容
9. 如图所示,质量为m的小环套在竖直固定的光滑直杆上,用轻绳跨过质量不计的光滑定滑轮与质量为2m的重物相连,定滑轮与直杆的距离为d,现将小环从与定滑轮等高的A处由静止释放,下列说法正确的是(重力加速度为g)( )
如图所示,质量为m的小环套在竖直固定的光滑直杆上,用轻绳跨过质量不计的光滑定滑轮与质量为2m的重物相连,定滑轮与直杆的距离为d,现将小环从与定滑轮等高的A处由静止释放,下列说法正确的是(重力加速度为g)( )| A. | 小环下滑过程中小环和重物组成的系统机械能守恒 | |
| B. | 当小环下落d的距离到达B点时,它的速度与重物上升速度大小之比为$\sqrt{2}$ | |
| C. | 小环到达B处时,重物上升的距离为d | |
| D. | 重物从开始运动到上升到最高的过程中,轻绳的张力始终大于2mg |
分析 由机械能守恒的条件:只有重力或弹力做功,判断系统的机械能是否守恒;小环在沿绳子方向的分速度与重物速度大小相等,将小环的速度沿绳子与垂直于绳子方向正交分解即可得到两者速度之比.由几何关系求小环到达B处时重物上升的距离.小环加速下落时重物加速上升,根据牛顿第二定律分析绳子的张力与2mg的关系.
解答 解:A、对于小环和重物组成的系统,由于只有重力做功,所以系统的机械能是守恒的.故A正确.
B、当小环下落d的距离到达B点时,将B的速度沿绳子方向和垂直于绳子方向分解,在沿绳子方向上的分速度等于重物的速度,有:v环cos45°=v重物,即得小环与重物速度之比为 v环:v重物=$\sqrt{2}$.故B正确;
C、小环到达B处时,绳子收缩的长度等于重物上升的高度,为 h=($\sqrt{2}$-1)d.故C错误.
D、重物从开始运动到上升到最高的过程中先向上做加速运动,后向上做减速运动,所以是先超重后失重,轻绳的张力先大于2mg,后小于2mg.故D错误.
故选:AB
点评 解决本题时应抓住:
①对与绳子牵连有关的问题,物体上的高度应等于绳子缩短的长度;
②小环的实际速度即为合速度,应将小环的速度沿绳子和垂直于绳子的方向正交分解,分析小环与重物的速度关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.小船在静水中的速度为4m/s,它要渡过一两岸平直,宽度为100m,水流速度为3m/s的河,则( )
| A. | 小船的轨迹不可能垂直河岸 | |
| B. | 小船渡河的时间可能为20s | |
| C. | 小船渡河的速度可能为8m/s | |
| D. | 小船以最短时间渡河,到达河对岸时被冲下75m远 |
19. 如图所示,两根间距为l的光滑平行金属导轨与水平面夹角为α,图中虚线下方区域内存在磁感应强度为B的匀强磁场,磁场方向垂直于导轨平面向上.两金属杆ab、cd的质量均为m,电阻均为R,垂直于导轨放置.开始时金属杆ab处在距磁场上边界一定距离处,金属杆cd处在导轨的最下端,被与导轨垂直的两根小柱挡住.现将金属杆ab由静止释放,当金属杆ab刚进入磁场便开始做匀速直线运动.已知重力加速度为g,则( )
如图所示,两根间距为l的光滑平行金属导轨与水平面夹角为α,图中虚线下方区域内存在磁感应强度为B的匀强磁场,磁场方向垂直于导轨平面向上.两金属杆ab、cd的质量均为m,电阻均为R,垂直于导轨放置.开始时金属杆ab处在距磁场上边界一定距离处,金属杆cd处在导轨的最下端,被与导轨垂直的两根小柱挡住.现将金属杆ab由静止释放,当金属杆ab刚进入磁场便开始做匀速直线运动.已知重力加速度为g,则( )
 如图所示,两根间距为l的光滑平行金属导轨与水平面夹角为α,图中虚线下方区域内存在磁感应强度为B的匀强磁场,磁场方向垂直于导轨平面向上.两金属杆ab、cd的质量均为m,电阻均为R,垂直于导轨放置.开始时金属杆ab处在距磁场上边界一定距离处,金属杆cd处在导轨的最下端,被与导轨垂直的两根小柱挡住.现将金属杆ab由静止释放,当金属杆ab刚进入磁场便开始做匀速直线运动.已知重力加速度为g,则( )
如图所示,两根间距为l的光滑平行金属导轨与水平面夹角为α,图中虚线下方区域内存在磁感应强度为B的匀强磁场,磁场方向垂直于导轨平面向上.两金属杆ab、cd的质量均为m,电阻均为R,垂直于导轨放置.开始时金属杆ab处在距磁场上边界一定距离处,金属杆cd处在导轨的最下端,被与导轨垂直的两根小柱挡住.现将金属杆ab由静止释放,当金属杆ab刚进入磁场便开始做匀速直线运动.已知重力加速度为g,则( )| A. | 金属杆ab进入磁场时感应电流的方向为由b到a | |
| B. | 金属杆ab进入磁场时速度大小为$\frac{2mgRsinα}{{{B^2}{l^2}}}$ | |
| C. | 金属杆ab进入磁场后产生的感应电动势为$\frac{mgsinα}{Bl}$ | |
| D. | 金属杆ab进入磁场后金属杆cd对两根小柱的压力大小为零 |
1. 如图所示,在倾角为30°的斜面上固定一电阻不计的光滑平行金属导轨,其间距为L,下端接有阻值为R的电阻,导轨处于匀强磁场中,磁感应强度大小为B,方向与斜面垂直(图中未画出).质量为m、阻值大小也为R的金属棒ab与固定在斜面上方的劲度系数为k的绝缘弹簧相接,弹簧处于原长并被锁定.现解除锁定的同时使金属棒获得沿斜面向下的速度v0,从开始运动到停止运动的过程中金属棒始终与导轨垂直并保持良好接触,弹簧始终在弹性限度内,重力加速度为g,在上述过程中( )
如图所示,在倾角为30°的斜面上固定一电阻不计的光滑平行金属导轨,其间距为L,下端接有阻值为R的电阻,导轨处于匀强磁场中,磁感应强度大小为B,方向与斜面垂直(图中未画出).质量为m、阻值大小也为R的金属棒ab与固定在斜面上方的劲度系数为k的绝缘弹簧相接,弹簧处于原长并被锁定.现解除锁定的同时使金属棒获得沿斜面向下的速度v0,从开始运动到停止运动的过程中金属棒始终与导轨垂直并保持良好接触,弹簧始终在弹性限度内,重力加速度为g,在上述过程中( )
 如图所示,在倾角为30°的斜面上固定一电阻不计的光滑平行金属导轨,其间距为L,下端接有阻值为R的电阻,导轨处于匀强磁场中,磁感应强度大小为B,方向与斜面垂直(图中未画出).质量为m、阻值大小也为R的金属棒ab与固定在斜面上方的劲度系数为k的绝缘弹簧相接,弹簧处于原长并被锁定.现解除锁定的同时使金属棒获得沿斜面向下的速度v0,从开始运动到停止运动的过程中金属棒始终与导轨垂直并保持良好接触,弹簧始终在弹性限度内,重力加速度为g,在上述过程中( )
如图所示,在倾角为30°的斜面上固定一电阻不计的光滑平行金属导轨,其间距为L,下端接有阻值为R的电阻,导轨处于匀强磁场中,磁感应强度大小为B,方向与斜面垂直(图中未画出).质量为m、阻值大小也为R的金属棒ab与固定在斜面上方的劲度系数为k的绝缘弹簧相接,弹簧处于原长并被锁定.现解除锁定的同时使金属棒获得沿斜面向下的速度v0,从开始运动到停止运动的过程中金属棒始终与导轨垂直并保持良好接触,弹簧始终在弹性限度内,重力加速度为g,在上述过程中( )| A. | 开始运动时金属棒与导轨接触点间电压为$\frac{BL{v}_{0}}{2}$ | |
| B. | 通过电阻R的最大电流一定是$\frac{BL{v}_{0}}{2R}$ | |
| C. | 通过电阻R的总电荷量为$\frac{mgBL}{2kR}$ | |
| D. | 回路产生的总热量小于$\frac{1}{2}$mv02+$\frac{{m}^{2}{g}^{2}}{4k}$ |
18. 如图所示,AB为固定的通电直导线,闭合导线框P与AB在同一平面内,当P远离AB运动时,导体框中产生的感应电流的情况是( )
如图所示,AB为固定的通电直导线,闭合导线框P与AB在同一平面内,当P远离AB运动时,导体框中产生的感应电流的情况是( )
 如图所示,AB为固定的通电直导线,闭合导线框P与AB在同一平面内,当P远离AB运动时,导体框中产生的感应电流的情况是( )
如图所示,AB为固定的通电直导线,闭合导线框P与AB在同一平面内,当P远离AB运动时,导体框中产生的感应电流的情况是( )| A. | 电流的方向是顺时针方向 | B. | 电流的方向是逆时针方向 | ||
| C. | 没有感应电流产生 | D. | 以上说法都不对 |
19.物体在合外力作用下做直线运动的v-t 图象如图所示,下列表述正确的是( )
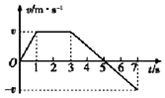

| A. | 在0~1s 内,物体做加速运动,合外力做正功 | |
| B. | 在1~3s 内,物体做匀速运动,合外力做正功 | |
| C. | 在3~7s 内,合外力做功为零 | |
| D. | 在0~5s 内,速度变化量为零,合力的平均功率为零 |
 如图所示,倾角θ=37°、质量M=5kg的斜面体A静置于水平地面上,可视作质点的小物块B的质量m=2kg.静置于斜面底端.与斜面间动摩擦因数μ=05,重力加速度取g=10m/s2.求:
如图所示,倾角θ=37°、质量M=5kg的斜面体A静置于水平地面上,可视作质点的小物块B的质量m=2kg.静置于斜面底端.与斜面间动摩擦因数μ=05,重力加速度取g=10m/s2.求:
 如图所示,在光滑绝缘的水平面上,一边长为10cm、电阻为1Ω、质量为0.1kg的正方形金属线框abcd以6$\sqrt{2}$m/s的速度向一有界磁场滑去,磁场方向与线框平面垂直,磁感应强度大小为0.5T,当线框全部进入磁场时,线框中已放出了1.8J的热量.则求
如图所示,在光滑绝缘的水平面上,一边长为10cm、电阻为1Ω、质量为0.1kg的正方形金属线框abcd以6$\sqrt{2}$m/s的速度向一有界磁场滑去,磁场方向与线框平面垂直,磁感应强度大小为0.5T,当线框全部进入磁场时,线框中已放出了1.8J的热量.则求