题目内容
3.某实验小组利用如图(a)所示的装置研究匀变速直线运动.他们将木块前端栓有不可伸长的细线,跨过固定在斜面边缘的小滑轮与重物相连,木块后面与打点计时器的纸带相连.起初木块停在靠近打点计时器的位置,重物到地面的距离小于木块到滑轮的距离.实验开始后,木块在重物的牵引下,由静止开始运动,重物落地后,小车会继续运动一段距离.打点计时器使用的交流电频率为50Hz.图(b)中甲、乙、丙是小车运动纸带上的三段,纸带运动方向如箭头所示.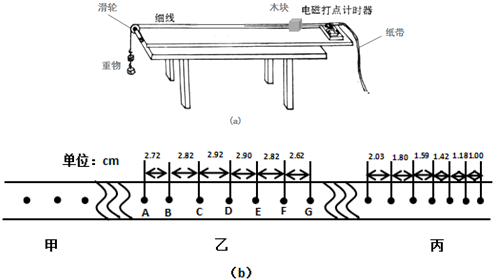
(1)开始试验时,应先启动打点计时器,再释放纸带.(填“先启动打点计时器,再释放纸带”或“先释放纸带,再启动打点计时器”)
(2)根据所提供纸带上的数据,乙段中打下B点时的瞬时速度大小为1.39m/s.逐差法计算丙段纸带时小车的加速度为5.06m/s2.(以上计算结果均保留三位有效数字)
(3)为了计算小车的加速度,还可以选择的最合理方法是C
A、根据任意两计数点的速度公式,用a=$\frac{△v}{△t}$算加速度
B、根据实验数据画出v-t图,量出其倾角α,由公式a=tanα求加速度
C、根据实验数据画出v-t图,由图上相距较远的两点,由a=$\frac{△v}{△t}$求a
D、依次算出通过连续两计数点间的加速度,算出其平均值为小车的加速度
(4)打甲段纸带时,小车的加速度是2.5m/s2.请根据加速度的情况,判断小车运动的最大速度可能出现在乙段纸带中的C.
| A、点D处 | B、点C处 | C、CD段之间 | D、DE段之间. |
分析 (1)实验时应先启动打点计时器,再释放纸带.
(2)根据某段时间内的平均速度等于中间时刻的瞬时速度求出B点的速度,根据连续相等时间内的位移之差是一恒量,运用逐差法求出加速度.
(3)通过题目给出的数据作出速度-时间图象,解出其斜率即是小车的加速度.误差最小.
(4)根据相等时间内的位移变化,确定速度最大的位置.
解答 解:(1)开始实验时,应先启动打点计时器,再释放纸带.
(2)B点的瞬时速度${v}_{B}=\frac{{x}_{AC}}{2T}=\frac{(2.72+2.82)×1{0}^{-2}}{0.04}m/s$≈1.39m/s,
根据△x=aT2,运用逐差法得,$a=\frac{(1.42+1.18+1.00-2.03-1.80-1.59)×1{0}^{-2}}{9×0.0{2}^{2}}$m/s2≈-5.06m/s2.
(3)A、在处理实验数据时,如果只使用其中两个数据,由于偶然误差的存在可能会造成最后误差较大;所以我们可以根据实验数据画出v-t图象,考虑到误差,不可能是所有点都整齐的排成一条直线,连线时,应该尽量使那些不能画在线上的点均匀地分布在线的两侧,这样图线上会舍弃误差较大的点,由图线上任意两点所对应的速度及时间,用公式a=$\frac{△v}{△t}$算出加速度,所以误差小,故A错误,C正确.
B、根据实验数据画出v-t图象,当纵坐标取不同的标度时,图象的倾角就会不同,所以量出其倾角,用公式a=tanα算出的数值并不是加速度,故B错误.
D、方法D也具有方法A相同的缺点,比如求解时,${a}_{1}=\frac{{v}_{2}-{v}_{1}}{T}$,${a}_{2}=\frac{{v}_{3}-{v}_{2}}{T}$,…${a}_{5}=\frac{{v}_{6}-{v}_{5}}{T}$,然后算出平均值a,求平均值时,$a=\frac{{v}_{6}-{v}_{1}}{5T}$,只用了v6和v1两组数据,偶然误差较大,故D错误.
故选:C.
(4)速度越来越大,相等时间内的位移越来越大,由于CD段的位移最大,则最大速度可能出现在乙纸带的CD段之间,故选:C.
故答案为:(1)先启动打点计时器,再释放纸带;(2)1.39,5.06,(3)C,(4)C.
点评 在实验中处理数据的方法较多,而图象法往往是一种比较准确的解题方法.以及掌握纸带的处理方法,会通过纸带求解瞬时速度和加速度,关键是匀变速直线运动推论的运用.

 用不同频率光照射某一金属发生光电效应时,光电子逸出最大初动能随入射光频率变化的图象如图所示,则图中横、纵轴截距及斜率的物理意义为( )
用不同频率光照射某一金属发生光电效应时,光电子逸出最大初动能随入射光频率变化的图象如图所示,则图中横、纵轴截距及斜率的物理意义为( )| A. | 斜率为普朗克常数的倒数 | B. | 纵轴截距为逸出功的倒数 | ||
| C. | 横轴截距为极限频率 | D. | 横轴截距为极限波长 |
| A. | 木星绕太阳运动的周期和轨道半径 | |
| B. | 木星绕太阳运动的周期和木星的半径 | |
| C. | 木星的卫星绕木星运动的周期和轨道半径 | |
| D. | 木星的卫星绕木星运动的周期和木星的半径 |
| A. | lg$\frac{a}{{a}_{0}}$=2lg$\frac{{R}_{0}}{R}$ | B. | lg$\frac{a}{{a}_{0}}$=$\frac{1}{2}$lg$\frac{{R}_{0}}{R}$ | C. | lg$\frac{v}{{v}_{0}}$=$\frac{1}{2}$lg$\frac{{R}_{0}}{R}$ | D. | lg$\frac{v}{{v}_{0}}$=$\frac{1}{2}$lg$\frac{R}{{R}_{0}}$ |
| A. | 该星球表面的重力加速度与地球表面重力加速度之比为1:9 | |
| B. | 该星球的密度与地球密度之比为4:9 | |
| C. | 该星球与地球第一宇宙速度之比为3:2 | |
| D. | 在该星球与地球上自相同高度处以相同初速度平抛物体的水平射程之比为1:1 |
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |

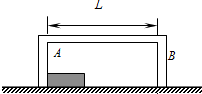 有一尺寸可忽略的木块放在足够长的水平粗糙地面上.取一无盖的长方形木盒B开口向下将A罩住.B的左右内壁间的距离为L=2m.开始时,A与B的左内壁相接触(如图所示),两者以相同的初速度v0向右,在摩擦力作用下,分别以大小为1m/s2和2m/s2的加速度做匀减速直线运动.若A和B能相撞.则相撞的结果是两者交换速度 (即撞后瞬间A和B的速度分别等于撞前瞬间B和A的速度,且撞击所用的时间极短可以忽略).A与B的其他侧面之间均无接触.重力加速度为g.
有一尺寸可忽略的木块放在足够长的水平粗糙地面上.取一无盖的长方形木盒B开口向下将A罩住.B的左右内壁间的距离为L=2m.开始时,A与B的左内壁相接触(如图所示),两者以相同的初速度v0向右,在摩擦力作用下,分别以大小为1m/s2和2m/s2的加速度做匀减速直线运动.若A和B能相撞.则相撞的结果是两者交换速度 (即撞后瞬间A和B的速度分别等于撞前瞬间B和A的速度,且撞击所用的时间极短可以忽略).A与B的其他侧面之间均无接触.重力加速度为g.