题目内容
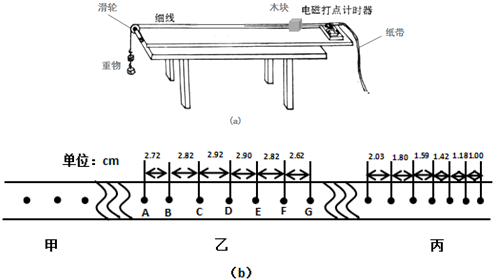
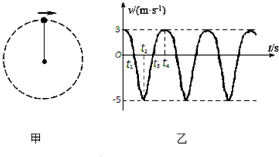
2.如图(a)所示,平行且光滑的长直金属导轨MN、PQ水平放置,间距L=0.4m.导轨右端接有阻值R=1Ω的电阻,导体棒垂直放置在导轨上,且接触良好,导体棒接入电路的电阻r=1Ω,导轨电阻不计,导轨间正方形区域abcd内有方向竖直向下的匀强磁场,bd连线与导轨垂直,长度也为L.从0时刻开始,磁感应强度B的大小随时间t变化,规律如图(b)所示;同一时刻,棒从导轨左端开始向右匀速运动,1s后刚好进入磁场,若使棒在导轨上始终以速度v=1m/s做直线运动,求:
(1)棒进入磁场前,电阻R中电流的大小和方向;
(2)棒通过abcd区域的过程中通过电阻R的电量;
(3)棒通过三角形abd区域时电流i与时间t的关系式.
分析 (1)根据法拉第电磁感应定律求出感应电动势大小,再求出电流大小,根据楞次定律判断电流方向;
(2)求通过电阻R的电量,需要先求出平均电动势,再求出平均电流,最后根据q=It,求出通过电阻R的电量;
(3)根据E=BLv求出回路中的瞬时电动势,再根据i=$\frac{E}{{R}_{总}}$.
解答 解:(1)进入磁场前,闭合回路中有磁场通过的有效面积不变,磁感应强度均匀变大,由法拉第电磁感应定律,回路中的电动势为:
$E=\frac{△BS}{△t}=0.04V$,
$I=\frac{E}{R+r}=0.02A$,
根据楞次定律判断,电流方向Q→N;
(2)棒通过abcd区域的过程中通过电阻R的电量为:$q=\overline It=\frac{\overline E}{R+r}t=\frac{△φ}{△t(R+r)}t=0.02C$
(3)根据几何关系可得:L有效=2(t-1)(1.0s≤t≤1.2s),
E=BL有效v,
$i=\frac{E}{R+r}=\frac{{B{L_{有效}}V}}{R+r}=\frac{1}{2}(t-1)A$ (1.0s≤t≤1.2s).
答:(1)棒进入磁场前,电阻R中电流的大小为0.02A,电流方向Q→N;
(2)棒通过abcd区域的过程中通过电阻R的电量0.02C;
(3)棒通过三角形abd区域时电流i与时间t的关系式$\frac{1}{2}(t-1)A$.
点评 本题考查了法拉第电磁感应定律和切割产生的感应电动势公式的运用,考查了闭合欧姆定律和求电量公式,综合程度较大.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
6.树上的苹果落向地球,针对这一现象,以下说法正确的是( )
| A. | 由于苹果质量小,对地球的引力小,而地球质量大,对苹果引力大 | |
| B. | 由于地球对苹果有引力,而苹果对地球无引力造成的 | |
| C. | 苹果对地球的引力大小和地球对苹果的引力大小是相等的 | |
| D. | 以上说法都不对 |
7. 劲度系数为k的轻弹簧,上端固定,下端挂一个质量为m的小球,小球静止时距地面高h.现用力向下拉球使球与地面接触,然后从静止释放小球,(假设弹簧始终在弹性限度内),下列说法中正确的是( )
劲度系数为k的轻弹簧,上端固定,下端挂一个质量为m的小球,小球静止时距地面高h.现用力向下拉球使球与地面接触,然后从静止释放小球,(假设弹簧始终在弹性限度内),下列说法中正确的是( )
 劲度系数为k的轻弹簧,上端固定,下端挂一个质量为m的小球,小球静止时距地面高h.现用力向下拉球使球与地面接触,然后从静止释放小球,(假设弹簧始终在弹性限度内),下列说法中正确的是( )
劲度系数为k的轻弹簧,上端固定,下端挂一个质量为m的小球,小球静止时距地面高h.现用力向下拉球使球与地面接触,然后从静止释放小球,(假设弹簧始终在弹性限度内),下列说法中正确的是( )| A. | 球在运动过程中距地面的最大高度为2h | |
| B. | 球上升过程中,系统势能不断增大 | |
| C. | 球距地面高度为h时,速度最大 | |
| D. | 球在运动过程中的最大加速度是$\frac{kh}{m}$ |
14. 如图所示,轻质弹簧竖直放置,下端固定.小球从弹簧的正上方某一高度处由静止下落,不计空气阻力,则从小球接触弹簧到弹簧被压缩至最短的过程中( )
如图所示,轻质弹簧竖直放置,下端固定.小球从弹簧的正上方某一高度处由静止下落,不计空气阻力,则从小球接触弹簧到弹簧被压缩至最短的过程中( )
 如图所示,轻质弹簧竖直放置,下端固定.小球从弹簧的正上方某一高度处由静止下落,不计空气阻力,则从小球接触弹簧到弹簧被压缩至最短的过程中( )
如图所示,轻质弹簧竖直放置,下端固定.小球从弹簧的正上方某一高度处由静止下落,不计空气阻力,则从小球接触弹簧到弹簧被压缩至最短的过程中( )| A. | 小球的机械能守恒 | B. | 小球的动能先增加后减小 | ||
| C. | 弹簧的弹性势能先增加后减小 | D. | 小球的重力势能一直减小 |
 如图所示,小明玩蹦蹦杆,在小明将蹦蹦杆中的弹簧向下压缩的过程中,小明的重力做正功,重力势能将减小,弹簧的弹力做负功,弹性势能将增加(选填“正”或“负”“增加”或“减少”)
如图所示,小明玩蹦蹦杆,在小明将蹦蹦杆中的弹簧向下压缩的过程中,小明的重力做正功,重力势能将减小,弹簧的弹力做负功,弹性势能将增加(选填“正”或“负”“增加”或“减少”)