题目内容
17. 如图所示,物块A静止在光滑水平面上,木板B和物块C一起以速度v0向右运动,与A发生弹性正碰,已知v0=5m/s,mA=6kg,mB=4kg,mC=2kg,C与B之间动摩擦因数μ=0.2,木板B足够长,取g=10m/s2,求:
如图所示,物块A静止在光滑水平面上,木板B和物块C一起以速度v0向右运动,与A发生弹性正碰,已知v0=5m/s,mA=6kg,mB=4kg,mC=2kg,C与B之间动摩擦因数μ=0.2,木板B足够长,取g=10m/s2,求:(1)B与A碰撞后A物块的速度;
(2)B、C共同的速度;
(3)整个过程中系统增加的内能.
分析 (1)对B与A弹性碰撞的过程,遵守动量守恒和机械能守恒,由动量守恒定律及机械能守恒定律定律可求得碰后A的速度;
(2)以B、C为研究对象,由动量守恒定律可求得BC共同的速度.
(3)运用能量守恒定律求增加的内能.
解答 解:(1)以AB为研究对象,B与A弹性碰撞过程,设向右为正,由动量守恒定律可有:
mBv0=mAvA+mBvB;
由机械能守恒定律可知:
$\frac{1}{2}$mBv02=$\frac{1}{2}$mBvB2+$\frac{1}{2}$mAvA2
联立解得:vA=4m/s;vB=-1m/s;
(2)碰后B反向,与C相互作用;对B、C,由动量守恒定律可知:
mCv0+mBvB=(mC+mB)v
解得:v=1m/s
(3)系统增加的内能为
Q=$\frac{1}{2}$mBvB2+$\frac{1}{2}$mCv02-$\frac{1}{2}$(mC+mB)v2
解得 Q=24J
答:
(1)B与A相碰后,A的速度为5m/s;
(2)BC共同的速度为1m/s.
(3)整个过程中系数增加的内能是24J.
点评 本题要分过程研究,知道弹性碰撞过程遵守两大守恒定律:动量守恒定律及机械能守恒定律,内能往往根据能量守恒定律求.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.下面说法中正确的是( )
| A. | 库仑利用扭秤实验测量出了万有引力常量G的大小 | |
| B. | 法拉第第一次发现电流的磁效应,并且制成了发电机 | |
| C. | 机械波在不同的介质中传播其频率不会发生改变 | |
| D. | 波长比障碍物尺寸小或相差不多时,会发生明显衍射现象 |
2. 如图所示,a、b是地球赤道上的两点,b、c是地球表面上不同纬度上的两点,若a、b、c三点随地球的自转都看作是匀速圆周运动,则下列说法中正确的是( )
如图所示,a、b是地球赤道上的两点,b、c是地球表面上不同纬度上的两点,若a、b、c三点随地球的自转都看作是匀速圆周运动,则下列说法中正确的是( )
 如图所示,a、b是地球赤道上的两点,b、c是地球表面上不同纬度上的两点,若a、b、c三点随地球的自转都看作是匀速圆周运动,则下列说法中正确的是( )
如图所示,a、b是地球赤道上的两点,b、c是地球表面上不同纬度上的两点,若a、b、c三点随地球的自转都看作是匀速圆周运动,则下列说法中正确的是( )| A. | a、b两点的角速度相同,而c点的角速度不同 | |
| B. | a、b两点的线速度大小相等 | |
| C. | b、c两点的线速度大小相等 | |
| D. | b、c两点的轨道半径相同 |
9.据报道在太阳系之外发现了一颗可能适合人类居住的类地行星Gliese581C,天文学观察发现绕该行星做圆周运动的卫星的轨道半径为月球绕地球做圆周运动半径的p倍,周期为月球绕地球做圆周运动周期的q倍.已知地球半径为R,表面重力加速度为g.万有引力常量为G,则该行星的质量为( )
| A. | $\frac{gR{p}^{2}}{G{p}^{3}}$ | B. | $\frac{g{R}^{2}{q}^{3}}{G{p}^{2}}$ | C. | $\frac{gR{q}^{2}}{G{p}^{3}}$ | D. | $\frac{g{R}^{2}{p}^{3}}{G{q}^{2}}$ |
6.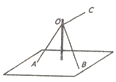 如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )
如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )
 如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )
如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )| A. | 20$\sqrt{3}$N | B. | 40N | C. | 40$\sqrt{3}$N | D. | 60N |
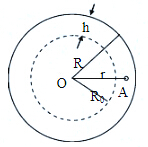 新发现行星,其星球半径为R=6400km,且由通常的水形成的海洋覆盖着它的所有表面,海洋的深度为h=10km,学者们对该行星进行探测时发现,当把试验用的样品浸入行星海洋的不同深度时,各处的自由落体加速度以相当高的精确度保持不变,已知万有引力常量G=6.67×10-11N•m2/kg2,海水密度ρ=1.0×103kg/m3,半径为R的球面面积公式S=4πR2.
新发现行星,其星球半径为R=6400km,且由通常的水形成的海洋覆盖着它的所有表面,海洋的深度为h=10km,学者们对该行星进行探测时发现,当把试验用的样品浸入行星海洋的不同深度时,各处的自由落体加速度以相当高的精确度保持不变,已知万有引力常量G=6.67×10-11N•m2/kg2,海水密度ρ=1.0×103kg/m3,半径为R的球面面积公式S=4πR2.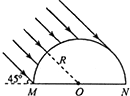 将长为l的玻璃圆柱体沿轴剖开后得到一块半圆柱体,其截面的正视图如图所示,MNPQ为其底面(PQ图中未画出),MN为直径.已知半圆的圆心为O、半径为R,玻璃的折射率n=$\sqrt{2}$.一束与MNPQ所在平面成45°且垂直于轴的平行光束射到半圆柱面上,经折射后,有部分光能从MNPQ面射出,忽略经多次反射到达MNPQ面的光线,求MNPQ透光部分的面积.
将长为l的玻璃圆柱体沿轴剖开后得到一块半圆柱体,其截面的正视图如图所示,MNPQ为其底面(PQ图中未画出),MN为直径.已知半圆的圆心为O、半径为R,玻璃的折射率n=$\sqrt{2}$.一束与MNPQ所在平面成45°且垂直于轴的平行光束射到半圆柱面上,经折射后,有部分光能从MNPQ面射出,忽略经多次反射到达MNPQ面的光线,求MNPQ透光部分的面积.