题目内容
6．
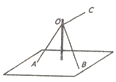如图所示，三根轻绳系于竖直杆上的同一点O，其中轻绳OA与OB等长且夹角为60°，竖直杆与平面AOB所成的角为30°．若轻绳OA、OB的拉力均为40N，要使杆受到绳子作用力的方向竖直向下，则水平轻绳OC的拉力大小为：（ ）| A． | 20$\sqrt{3}$N | B． | 40N | C． | 40$\sqrt{3}$N | D． | 60N |
分析 要使桩子受到绳子作用力方向竖直向下，则绳子OC与OA、OB的合力竖直向下，则绳子OA和OB的合力与OC对O的拉力和合力在水平面内平衡；根据平行四边形定则先求出AO和BO的合力，再结合要求分析即可．
解答 解：轻绳OA与OB等长且夹角为60°，则它们的合力：${F}_{1}=2Fcos\frac{60°}{2}=\sqrt{3}F=40\sqrt{3}N$，
OA与OB的合力沿水平方向的分力与竖直方向之间的夹角是30°，所以：${F}_{x}={F}_{1}sin30°=20\sqrt{3}N$，故A正确，BCD错误．
故选：A
点评 本题关键是灵活选择研究对象，然后根据共点力平衡条件结合矢量的合成的方法分析即可．
练习册系列答案
相关题目
如图所示，物块A静止在光滑水平面上，木板B和物块C一起以速度v0向右运动，与A发生弹性正碰，已知v0=5m/s，mA=6kg，mB=4kg，mC=2kg，C与B之间动摩擦因数μ=0.2，木板B足够长，取g=10m/s2，求：
14．嫦娥五号探测器预计在2017年由长征五号运载火箭执行发射，全面完成探月工程绕月、落月、返回地球的总目标．已知地球半径为月球的3.7倍，地球表面的重力加速度约为月球表面重力加速度的6倍，已知地球的第一宇宙速度为7.9km/s，则月球的第一宇宙速度约为（ ）
| A． | 0.36km/s | B． | 0.87km/s | C． | 1.32km/s | D． | 1.68km/s |
一位同学利用光电加速器等器材做实验来验证自由落体运动是匀变速直线运动，如图甲所示，该同学让一直径为d、质量为m的金属小球从O处由静止释放，下落过程中能通过O处正下方，固定于M处的光电门，测得O、M间的距离为H（H＞＞d），光电计时器记录下小球通过光电门的时间为t，当地的重力加速度为g．
11．下列陈述中不符合历史事实的是（ ）
| A． | 安培首先提出了磁场对运动电荷有力作用 | |
| B． | 牛顿是在伽利略理想斜面实验的基础上进行假想推理得出了牛顿第一定律 | |
| C． | 法拉第提出了场的概念并用电场线形象地描述电场 | |
| D． | 奥斯特首先发现了电和磁有联系 |
18．据报道，我国将于2016年择机发射“天宫二号”，并计划于2020年发射“火星探测器”．设“天宫二号”绕地球做圆周运动的半径为r1、周期为T1；“火星探测器”绕火星做做圆周运动的半径为r2、周期为T2，万有引力常量为G．根据题设条件可得（ ）
| A． | 关系式$\frac{{{r}_{1}}^{3}}{{{T}_{1}}^{2}}$=$\frac{{{r}_{2}}^{3}}{{{T}_{2}}^{2}}$ | |
| B． | 地球与火星的平均密度之比为$\frac{{{T}_{1}}^{2}}{{{T}_{2}}^{2}}$ | |
| C． | 地球与火星的质量之比为$\frac{{{r}_{1}}^{3}{{T}_{2}}^{2}}{{{r}_{2}}^{3}{{T}_{1}}^{2}}$ | |
| D． | “天宫二号”和“火星探测器”的向心加速度大小之比为$\frac{{r}_{1}{{T}_{2}}^{2}}{{r}_{2}{{T}_{1}}^{2}}$ |
如图所示为利用医用吊瓶水平喷出的细水柱显示平抛轨进的实验．关于这个实验．下列说法正确的是BC