��Ŀ����
7��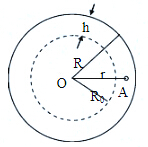 �·������ǣ�������뾶ΪR=6400km������ͨ����ˮ�γɵĺ������������б��棬��������Ϊh=10km��ѧ���ǶԸ����ǽ���̽��ʱ���֣����������õ���Ʒ�������Ǻ���IJ�ͬ���ʱ������������������ٶ����൱�ߵľ�ȷ�ȱ��ֲ��䣬��֪������������G=6.67��10-11N•m2/kg2����ˮ�ܶȦ�=1.0��103kg/m3���뾶ΪR�����������ʽS=4��R2��
�·������ǣ�������뾶ΪR=6400km������ͨ����ˮ�γɵĺ������������б��棬��������Ϊh=10km��ѧ���ǶԸ����ǽ���̽��ʱ���֣����������õ���Ʒ�������Ǻ���IJ�ͬ���ʱ������������������ٶ����൱�ߵľ�ȷ�ȱ��ֲ��䣬��֪������������G=6.67��10-11N•m2/kg2����ˮ�ܶȦ�=1.0��103kg/m3���뾶ΪR�����������ʽS=4��R2������ʾ�����������Ŀ�ǻ�ڣ�����λ�õ��ʵ��ܵ���ǵ���������Ϊ�㣩
�ٴ�������溣ˮ������ԼΪ���٣�����R���ѡ�h��ĸ��ʾ��
�ڴ����DZ��洦������������ٶ�ԼΪ���٣�
���� ��1������ˮ������ٸ���m=��V������
��2�����������������������������������������ٶ�
��� �⣺��1����R��${R}_{0}^{\;}$�ֱ��ʾ�����������������ڲ㣨�����㺣���⣩�İ뾶��r��ʾ����������һ��A���������ĵľ��룬��
${R}_{0}^{\;}��r��R$
��${R}_{\;}^{\;}={R}_{0}^{\;}+h$
�������������ΪM��ˮ���ܶ�Ϊ�ѣ�����hԶС��R������������溣����������ɱ�ʾΪ
$m=4��{R}_{0}^{2}h�ѡ�4��{R}_{\;}^{2}h��$
��2����$G\frac{Mm}{{R}_{\;}^{2}}=m{g}_{��}^{\;}$��${g}_{��}^{\;}=\frac{GM}{{R}_{\;}^{2}}$
$G\frac{��M-m��m}{{R}_{0}^{2}}=m{g}_{0}^{\;}$��${g}_{0}^{\;}=\frac{G��M-m��}{{R}_{0}^{2}}$
�����⣺${g}_{��}^{\;}={g}_{0}^{\;}$������$\frac{M}{{R}_{\;}^{2}}=\frac{��M-m��}{{R}_{0}^{2}}=\frac{��M-m��}{��R-h��_{\;}^{2}}•M$=$\frac{{R}_{\;}^{2}m}{2Rh-{h}_{\;}^{2}}$
��${g}_{��}^{\;}=\frac{G��4��{��}_{ˮ}^{\;}{R}_{\;}^{2}h}{{R}_{\;}^{2}•2h}=2��G{��}_{ˮ}^{\;}R$
��$G=6.67��1{0}_{\;}^{-11}N•{m}_{\;}^{2}/k{g}_{\;}^{2}$��${��}_{ˮ}^{\;}=1.0��1{0}_{\;}^{3}kg/{m}_{\;}^{3}$��$R=6.4��1{0}_{\;}^{6}m$����ã�${g}_{��}^{\;}=2.7m/{s}_{\;}^{2}$
�𣺢ٴ�������溣ˮ������ԼΪ$4��{R}_{\;}^{2}h��$
�ڴ����DZ��洦������������ٶ�ԼΪ$2.7m/{s}_{\;}^{2}$
���� �Ȿ��Ĺؼ�����������Ҫ��������������˶����ǣ��������û�������ʽ�����DZ��洦������������ٶȣ�����ˮ��Ϊ�˶�����Ⱥ����ؼ�����������������������

 ��У����ϵ�д�
��У����ϵ�д� ��ͼ��ʾ������ƽֱ�ĺӰ���v�������ߣ���ͨ�������쳤�����ϴ����������ķ����н����˹�������ʼ����ˮ��ƽ�У�������˵����ȷ���ǣ�������
��ͼ��ʾ������ƽֱ�ĺӰ���v�������ߣ���ͨ�������쳤�����ϴ����������ķ����н����˹�������ʼ����ˮ��ƽ�У�������˵����ȷ���ǣ�������| A�� | ���ڿ���ǰ�������ȱ����˶� | |
| B�� | ���ڿ���ǰ���˶��켣��ֱ�� | |
| C�� | ������Ӱ��ļн�Ϊ��ʱ����������Ϊvcos�� | |
| D�� | ������Ӱ��ļн�Ϊ��ʱ����������Ϊ$\frac{v}{cos��}$ |
| A�� | �������ɽǶȣ������ߣ����ȱ���ֱ���˶��ĺ��˶�һ�����ȱ���ֱ���˶� | |
| B�� | ����Բ���˶��Ǽ��ٶȲ���������˶� | |
| C�� | ţ��������֮���ձ����������Ϊ���ݣ��������ܵ��������������������������ɲ��ⶨ��������������G | |
| D�� | ������̫����ת�˶�����뾶R�����η���������T��ƽ��֮��Ϊ��������$\frac{{R}^{3}}{{T}^{2}}$=k����ôk�Ĵ�Сֻ��̫���������йأ������������� |
 ��ͼ��ʾ��P��QΪij����ˮƽ�����ϵ����㣬��P�����·�һ���������ڴ�����ʯ�ͣ��ٶ�������Χ��ʯ���ȷֲ����ܶ�Ϊ�ѣ�ʯ���ܶ�ԶС�ڦѣ��ɽ���������������Ϊ��ǻ�����û����һ��ǻ����õ����������ٶȣ�����ֵ������ֱ�������ڿ�ǻʱ���õ����������ٶȵĴ�С�ͷ���������������Сƫ�룬�������ٶ���ԭ��ֱ����PO�����ϵ�ͶӰ���������ֵ��ƫ��������������ٶȷ��� ����Ϊ��̽Ѱʯ�������λ�ú�ʯ�ʹ�����������P�㵽�����������ٶȷ���������֪��������ΪG��������˵����ȷ���ǣ�������
��ͼ��ʾ��P��QΪij����ˮƽ�����ϵ����㣬��P�����·�һ���������ڴ�����ʯ�ͣ��ٶ�������Χ��ʯ���ȷֲ����ܶ�Ϊ�ѣ�ʯ���ܶ�ԶС�ڦѣ��ɽ���������������Ϊ��ǻ�����û����һ��ǻ����õ����������ٶȣ�����ֵ������ֱ�������ڿ�ǻʱ���õ����������ٶȵĴ�С�ͷ���������������Сƫ�룬�������ٶ���ԭ��ֱ����PO�����ϵ�ͶӰ���������ֵ��ƫ��������������ٶȷ��� ����Ϊ��̽Ѱʯ�������λ�ú�ʯ�ʹ�����������P�㵽�����������ٶȷ���������֪��������ΪG��������˵����ȷ���ǣ�������| A�� | ��ʯ�ͻᵼ��P���������ٶ�ƫС | |
| B�� | ��ʯ�ͻᵼ��P���������ٶ�ƫ�� | |
| C�� | ��ͼ��P���������ٶȷ���ֵ����Q���������ٶȷ���ֵ | |
| D�� | Q���������ٶȷ���ֵԼΪ��g=$\frac{G��Vd}{��{d}^{2}+{x}^{2}��^{\frac{3}{2}}}$ |
 ��ͼ��ʾ����������ֱƽ���ڵ�$\frac{1}{4}$Բ���AB��O��ΪԲ�ģ�OAˮƽ��OB��ֱ���뾶Ϊ2$\sqrt{2}$m����O����OA�׳�һС��С�����Բ��AB�ϵ��е�C��vt�ķ����ӳ�����OB���ӳ����ཻ��D�㣮��֪�������ٶ�g=10m/s2����
��ͼ��ʾ����������ֱƽ���ڵ�$\frac{1}{4}$Բ���AB��O��ΪԲ�ģ�OAˮƽ��OB��ֱ���뾶Ϊ2$\sqrt{2}$m����O����OA�׳�һС��С�����Բ��AB�ϵ��е�C��vt�ķ����ӳ�����OB���ӳ����ཻ��D�㣮��֪�������ٶ�g=10m/s2���� һ������ӹ⻬б��Eh=1.8m��A�㴦�ɾ�ֹ���£�Ȼ���ڴֲ�ˮƽ���ϻ���һ�ξ����ֹͣ����ͼ��ʾ�����������廬��б��˵���ײ���ã���ˮƽ���������Ķ�Ħ������Ϊ��=0.2����ѡ��ˮƽ��Ϊ�������棬��
һ������ӹ⻬б��Eh=1.8m��A�㴦�ɾ�ֹ���£�Ȼ���ڴֲ�ˮƽ���ϻ���һ�ξ����ֹͣ����ͼ��ʾ�����������廬��б��˵���ײ���ã���ˮƽ���������Ķ�Ħ������Ϊ��=0.2����ѡ��ˮƽ��Ϊ�������棬�� 2014��12��12�գ�ӡ����צ��ʡ�İ���ڼ�������Ϊ���յı���������ʯ���ֺ�������˾���ʧ����ͼ��ʾ������Ϊ�ʵ��һ��ʯͷ�ӷ�����ʯ���ĸ�AB=5m����AC=50m��ɽ�����ɾ�ֹ���£�������ʯͷ����������������Ħ��������Ӱ�죬ɽ��
2014��12��12�գ�ӡ����צ��ʡ�İ���ڼ�������Ϊ���յı���������ʯ���ֺ�������˾���ʧ����ͼ��ʾ������Ϊ�ʵ��һ��ʯͷ�ӷ�����ʯ���ĸ�AB=5m����AC=50m��ɽ�����ɾ�ֹ���£�������ʯͷ����������������Ħ��������Ӱ�죬ɽ�� ��ͼ��ʾ�����A��ֹ�ڹ⻬ˮƽ���ϣ�ľ��B�����Cһ�����ٶ�v0�����˶�����A����������������֪v0=5m/s��mA=6kg��mB=4kg��mC=2kg��C��B֮�䶯Ħ��������=0.2��ľ��B�㹻����ȡg=10m/s2����
��ͼ��ʾ�����A��ֹ�ڹ⻬ˮƽ���ϣ�ľ��B�����Cһ�����ٶ�v0�����˶�����A����������������֪v0=5m/s��mA=6kg��mB=4kg��mC=2kg��C��B֮�䶯Ħ��������=0.2��ľ��B�㹻����ȡg=10m/s2����