题目内容
12.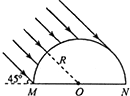 将长为l的玻璃圆柱体沿轴剖开后得到一块半圆柱体,其截面的正视图如图所示,MNPQ为其底面(PQ图中未画出),MN为直径.已知半圆的圆心为O、半径为R,玻璃的折射率n=$\sqrt{2}$.一束与MNPQ所在平面成45°且垂直于轴的平行光束射到半圆柱面上,经折射后,有部分光能从MNPQ面射出,忽略经多次反射到达MNPQ面的光线,求MNPQ透光部分的面积.
将长为l的玻璃圆柱体沿轴剖开后得到一块半圆柱体,其截面的正视图如图所示,MNPQ为其底面(PQ图中未画出),MN为直径.已知半圆的圆心为O、半径为R,玻璃的折射率n=$\sqrt{2}$.一束与MNPQ所在平面成45°且垂直于轴的平行光束射到半圆柱面上,经折射后,有部分光能从MNPQ面射出,忽略经多次反射到达MNPQ面的光线,求MNPQ透光部分的面积.
分析 光线射到MN上时会发生全反射现象,从而不能从MN射出;根据临界角公式sinC=$\frac{1}{n}$求出临界角C,根据几何关系确定能从MN射出的光线范围,由几何知识求解面积.
解答 解:设光由介质射向空气的临界角为C.
由 sinC=$\frac{1}{n}$,得 C=45°
从A点进入玻璃砖的光线垂直半球面,沿半径AO直达球心O,且入射角等于临界角,恰好在O点发生全反射,A点左侧的光线经球面折射后,射在MN上的入射角都大于临界角,在MN上全反射,不能从MN上射出.A点右侧光线一直到与球面正好相切的范围内的光线经球面折射后,在MN上的入射角均小于临界角,都能从MN上射出,它们在MN上的出射宽度就是OD.
由折射定律得
$\frac{sini}{sinr}$=n
MN上透光部分的长度:
OD=Rsinr
MNPQ平面内透光部分面积为:
S=OD•l=$\frac{\sqrt{2}}{2}$Rl
答:MNPQ透光部分的面积为$\frac{\sqrt{2}}{2}$Rl.
点评 解决本题的关键要掌握全反射及其产生条件,结合几何知识确定边界光线,要规范作图,有利于答题.

练习册系列答案
相关题目
20.若一气泡从湖底上升到湖面的过程中温度保持不变,则在此过程中关于气泡中的气体,下列说法正确的是( )
| A. | 气体分子间的作用力增大 | B. | 气体分子的平均速率增大 | ||
| C. | 气体分子的平均动能减小 | D. | 气泡的体积增大 |
7. 人字梯(也称A型梯),因其使用时梯杆及地面构成一个等腰三角形,看起来像一个“人”字,因而得名(如图甲).图乙是可升降人字梯简化的正视图,每根梯杆由两部分组成,类似拉杆箱的拉杆可长短伸缩.梯杆的顶端有轴将两侧梯杆连在一起,使两侧梯杆可绕O转动.为了安全,梯杆的下端PQ两点用长度一定的安全拉绳固定,拉直时安全绳水平.设水平地面光滑,不考虑梯子自身的重量,当质量一定的人站在梯顶时,由于需要将人字梯的升降杆拉出使其升高,则升高后和升高前相比( )
人字梯(也称A型梯),因其使用时梯杆及地面构成一个等腰三角形,看起来像一个“人”字,因而得名(如图甲).图乙是可升降人字梯简化的正视图,每根梯杆由两部分组成,类似拉杆箱的拉杆可长短伸缩.梯杆的顶端有轴将两侧梯杆连在一起,使两侧梯杆可绕O转动.为了安全,梯杆的下端PQ两点用长度一定的安全拉绳固定,拉直时安全绳水平.设水平地面光滑,不考虑梯子自身的重量,当质量一定的人站在梯顶时,由于需要将人字梯的升降杆拉出使其升高,则升高后和升高前相比( )
 人字梯(也称A型梯),因其使用时梯杆及地面构成一个等腰三角形,看起来像一个“人”字,因而得名(如图甲).图乙是可升降人字梯简化的正视图,每根梯杆由两部分组成,类似拉杆箱的拉杆可长短伸缩.梯杆的顶端有轴将两侧梯杆连在一起,使两侧梯杆可绕O转动.为了安全,梯杆的下端PQ两点用长度一定的安全拉绳固定,拉直时安全绳水平.设水平地面光滑,不考虑梯子自身的重量,当质量一定的人站在梯顶时,由于需要将人字梯的升降杆拉出使其升高,则升高后和升高前相比( )
人字梯(也称A型梯),因其使用时梯杆及地面构成一个等腰三角形,看起来像一个“人”字,因而得名(如图甲).图乙是可升降人字梯简化的正视图,每根梯杆由两部分组成,类似拉杆箱的拉杆可长短伸缩.梯杆的顶端有轴将两侧梯杆连在一起,使两侧梯杆可绕O转动.为了安全,梯杆的下端PQ两点用长度一定的安全拉绳固定,拉直时安全绳水平.设水平地面光滑,不考虑梯子自身的重量,当质量一定的人站在梯顶时,由于需要将人字梯的升降杆拉出使其升高,则升高后和升高前相比( )| A. | 梯子对地面的压力增大 | B. | 梯子对地面的压力减小 | ||
| C. | 人对左侧梯杆的压力增大 | D. | 安全绳的张力减小 |
 2014年12月12日,印尼中爪哇省的班查内加拉县因为连日的暴雨引发泥石流灾害,造成了巨大损失.如图所示,可视为质点的一个石头从发生泥石流的高AB=5m、长AC=50m的山坡上由静止滚下,不考虑石头在整个滚动过程中摩擦阻力的影响,山坡
2014年12月12日,印尼中爪哇省的班查内加拉县因为连日的暴雨引发泥石流灾害,造成了巨大损失.如图所示,可视为质点的一个石头从发生泥石流的高AB=5m、长AC=50m的山坡上由静止滚下,不考虑石头在整个滚动过程中摩擦阻力的影响,山坡 如图所示,物块A静止在光滑水平面上,木板B和物块C一起以速度v0向右运动,与A发生弹性正碰,已知v0=5m/s,mA=6kg,mB=4kg,mC=2kg,C与B之间动摩擦因数μ=0.2,木板B足够长,取g=10m/s2,求:
如图所示,物块A静止在光滑水平面上,木板B和物块C一起以速度v0向右运动,与A发生弹性正碰,已知v0=5m/s,mA=6kg,mB=4kg,mC=2kg,C与B之间动摩擦因数μ=0.2,木板B足够长,取g=10m/s2,求: 一位同学利用光电加速器等器材做实验来验证自由落体运动是匀变速直线运动,如图甲所示,该同学让一直径为d、质量为m的金属小球从O处由静止释放,下落过程中能通过O处正下方,固定于M处的光电门,测得O、M间的距离为H(H>>d),光电计时器记录下小球通过光电门的时间为t,当地的重力加速度为g.
一位同学利用光电加速器等器材做实验来验证自由落体运动是匀变速直线运动,如图甲所示,该同学让一直径为d、质量为m的金属小球从O处由静止释放,下落过程中能通过O处正下方,固定于M处的光电门,测得O、M间的距离为H(H>>d),光电计时器记录下小球通过光电门的时间为t,当地的重力加速度为g. 如图所示,闭合线圈abcd竖直放置在匀强磁场中,线圈的匝数为100匝.开始时线圈静止不动,然后线圈从图示位置绕转动轴OO′旋转90°,所用时间为0.5s,穿过线圈的磁通量变化量为0.08Wb.问:
如图所示,闭合线圈abcd竖直放置在匀强磁场中,线圈的匝数为100匝.开始时线圈静止不动,然后线圈从图示位置绕转动轴OO′旋转90°,所用时间为0.5s,穿过线圈的磁通量变化量为0.08Wb.问: