题目内容
11. 如图所示,光滑导热活塞C将体积为V0的导热容器分成A、B两室,A、B中各封有一定质量的同种气体,A室左侧连接有一U形气压计(U形管内气体的体积忽略不计),B室右侧有一阀门K,可与外界大气相通,外界大气压等于76cmHg,气温恒定.当光滑导热活塞C静止时,A、B两室容积相等,气压计水银柱高度差为38cm.现将阀门K打开,当活塞C不再移动时,求:
如图所示,光滑导热活塞C将体积为V0的导热容器分成A、B两室,A、B中各封有一定质量的同种气体,A室左侧连接有一U形气压计(U形管内气体的体积忽略不计),B室右侧有一阀门K,可与外界大气相通,外界大气压等于76cmHg,气温恒定.当光滑导热活塞C静止时,A、B两室容积相等,气压计水银柱高度差为38cm.现将阀门K打开,当活塞C不再移动时,求:①A室的体积;
②B室从阀门K逸出的气体质量与原有质量的比.
分析 ①A中气体前后变化为等温变化,对A中气体运用玻意耳定律即可求出A室的体积;
②利用状态相同的同种气体的质量比等于体积比,即可求出B室从阀门K逸出的气体质量与原有质量的比.
解答 解:①阀门K闭合,A室的体积为:${V_A}=\frac{1}{2}{V_0}$
压强:pA=(76+38)cmH=114cmHg
设阀门K打开,A室的体积为${V_A}^′$
压强:${p_A}^′=76cmHg$
等温变化,对A中气体运用玻意耳定律可得:${p_A}{V_A}={p_A}^′{V_A}^′$
解得:${V_A}^′=0.75{V_0}$
②阀门K打开后,若B室气体的质量不变,B室的体积为:${V_B}^′=0.75{V_0}$
由于B室的气体逸出,留在B室的气体体积为:0.25V0
B室从阀门K逸出的气体质量与原有质量的比为:$\frac{{0.75{V_0}-0.25{V_0}}}{{0.75{V_0}}}=\frac{2}{3}$
答:①A室的体积为0.75V0;
②B室从阀门K逸出的气体质量与原有质量的比为$\frac{2}{3}$.
点评 本题考查气体定律的运用,解题关键是要分析好压强、体积、温度三个参量的变化情况,选择合适的规律解决,难度不大,第②问解决的关键是要会利用状态相同的同种气体的质量比等于体积比.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
2. 如图所示,0点有一粒子源,在某时刻发射大量质量为m,电荷量为q的带正电的粒子,它们的速度大小相等、速度方向均在xOy平面内;在直线x=a与x=2a之间,在垂直于xOy平面向外的磁感应强度为B的匀强磁场,与y轴正方向成60°角发射的粒子恰好垂直于磁场右边界射出.不计粒子的重力和粒子间的相互作用力.关于这些粒子的运动,下列说法正确的是( )
如图所示,0点有一粒子源,在某时刻发射大量质量为m,电荷量为q的带正电的粒子,它们的速度大小相等、速度方向均在xOy平面内;在直线x=a与x=2a之间,在垂直于xOy平面向外的磁感应强度为B的匀强磁场,与y轴正方向成60°角发射的粒子恰好垂直于磁场右边界射出.不计粒子的重力和粒子间的相互作用力.关于这些粒子的运动,下列说法正确的是( )
 如图所示,0点有一粒子源,在某时刻发射大量质量为m,电荷量为q的带正电的粒子,它们的速度大小相等、速度方向均在xOy平面内;在直线x=a与x=2a之间,在垂直于xOy平面向外的磁感应强度为B的匀强磁场,与y轴正方向成60°角发射的粒子恰好垂直于磁场右边界射出.不计粒子的重力和粒子间的相互作用力.关于这些粒子的运动,下列说法正确的是( )
如图所示,0点有一粒子源,在某时刻发射大量质量为m,电荷量为q的带正电的粒子,它们的速度大小相等、速度方向均在xOy平面内;在直线x=a与x=2a之间,在垂直于xOy平面向外的磁感应强度为B的匀强磁场,与y轴正方向成60°角发射的粒子恰好垂直于磁场右边界射出.不计粒子的重力和粒子间的相互作用力.关于这些粒子的运动,下列说法正确的是( )| A. | 粒子的速度大小为$\frac{aBq}{m}$ | |
| B. | 粒子的速度大小为$\frac{2aBq}{m}$ | |
| C. | 与y轴正方向成90°角射出的粒子在磁场中运动的时间最长 | |
| D. | 与y轴正方向成120°角射出的粒子在磁场中运动的时间最长 |
3.下列关于物体动量和冲量的说法中正确的是( )
| A. | 物体所受合外力冲量越大,它的动量就越大 | |
| B. | 物体所受合外力冲量不为零,它的动量一定变化 | |
| C. | 物体动量变化的方向,就是合力冲量的方向 | |
| D. | 物体所受合外力越大,它的动量变化就越快 |
 一组不知方向的匀强电场的电场线(与水平方向成60°角),把1×10-6C的负电荷从A点沿水平线移到B点.静电力作了2×10-6J的功.A、B两点间的距离为2cm,求:匀强电场的场强为多大?方向如何?
一组不知方向的匀强电场的电场线(与水平方向成60°角),把1×10-6C的负电荷从A点沿水平线移到B点.静电力作了2×10-6J的功.A、B两点间的距离为2cm,求:匀强电场的场强为多大?方向如何?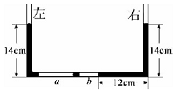 如图,粗细均匀的U型玻璃管两端开口,底部的水平管内有长度分别为10cm、5cm的两段空气柱a、b,左右两管竖直,水银柱的长度如图中标注所示,在左管内缓慢注入一定量的水银,稳定后右管的水银面比原来高h=10cm,已知大气压强P0=76cmHg,环境稳定恒定,求向左管注入的水银柱长度.
如图,粗细均匀的U型玻璃管两端开口,底部的水平管内有长度分别为10cm、5cm的两段空气柱a、b,左右两管竖直,水银柱的长度如图中标注所示,在左管内缓慢注入一定量的水银,稳定后右管的水银面比原来高h=10cm,已知大气压强P0=76cmHg,环境稳定恒定,求向左管注入的水银柱长度. 自动称米机已在许多粮食加工厂广泛使用.有人认为:因米流落到容器中时有向下的冲力而导致装的分量不足;也有人则认为:当预定米的质量数满足时,自动装置即刻切断米流时,此刻尚有一些米仍在空中,这些米是多装袋的.因而双方争执起来,究竟哪种说法对呢?
自动称米机已在许多粮食加工厂广泛使用.有人认为:因米流落到容器中时有向下的冲力而导致装的分量不足;也有人则认为:当预定米的质量数满足时,自动装置即刻切断米流时,此刻尚有一些米仍在空中,这些米是多装袋的.因而双方争执起来,究竟哪种说法对呢? 如图所示,长为$\sqrt{3}$L的轻绳,两端分别固定在一根竖直棒上相距为L的A、B两点,一个质量为m的光滑小圆环套在绳子上,当竖直棒以一定的角速度转动时,圆环以A为圆心在水平面上作匀速圆周运动,则
如图所示,长为$\sqrt{3}$L的轻绳,两端分别固定在一根竖直棒上相距为L的A、B两点,一个质量为m的光滑小圆环套在绳子上,当竖直棒以一定的角速度转动时,圆环以A为圆心在水平面上作匀速圆周运动,则 在北京西郊,有一座神秘的城堡,它就是我国的宇航员培训基地,也是世界上第3座大规模的航天城、如图是航天城中最快能$\frac{π}{2}$s转一圈的宇航员训练用的离心机,训练时离心机在水平面内绕竖直轴转动,离心机里的航天员与转轴的距离为L=8m.已知航天员的质量为60kg,重力加速度为g=l0m/s2.当离心机以最大角速度匀速转 动时,求:
在北京西郊,有一座神秘的城堡,它就是我国的宇航员培训基地,也是世界上第3座大规模的航天城、如图是航天城中最快能$\frac{π}{2}$s转一圈的宇航员训练用的离心机,训练时离心机在水平面内绕竖直轴转动,离心机里的航天员与转轴的距离为L=8m.已知航天员的质量为60kg,重力加速度为g=l0m/s2.当离心机以最大角速度匀速转 动时,求: 如图所示,光滑杆偏离竖直方向的夹角为θ,杆以O为支点绕竖直线旋转,质量为m的小球套在杆上可沿杆滑动.当杆角速度为ω1时,小球旋转平面在A处,球对杆的压力为N1;当杆角速度为ω2时,小球旋转平面在B处,球对杆的压力为N2,则有( )
如图所示,光滑杆偏离竖直方向的夹角为θ,杆以O为支点绕竖直线旋转,质量为m的小球套在杆上可沿杆滑动.当杆角速度为ω1时,小球旋转平面在A处,球对杆的压力为N1;当杆角速度为ω2时,小球旋转平面在B处,球对杆的压力为N2,则有( )