题目内容
16. 如图所示,长为$\sqrt{3}$L的轻绳,两端分别固定在一根竖直棒上相距为L的A、B两点,一个质量为m的光滑小圆环套在绳子上,当竖直棒以一定的角速度转动时,圆环以A为圆心在水平面上作匀速圆周运动,则
如图所示,长为$\sqrt{3}$L的轻绳,两端分别固定在一根竖直棒上相距为L的A、B两点,一个质量为m的光滑小圆环套在绳子上,当竖直棒以一定的角速度转动时,圆环以A为圆心在水平面上作匀速圆周运动,则(1)求此时轻绳上的张力T大小;
(2)竖直棒转动的角速ω.
(3)A点距地面高为$\frac{3L}{2}$,若某时刻轻绳从环处断掉则求环落在水平地面上的区域范围.
分析 (1、2)根据几何关系求出环做圆周运动的半径,抓住小球竖直上合力为零,水平方向上的合力提供向心力,求出绳子的张力大小和角速度的大小.
(3)轻绳断掉后,环做平抛运动,根据高度求出平抛运动的时间,结合线速度的大小求出平抛运动的水平位移,根据几何关系求出环落在水平地面上的区域范围.
解答 解:(1、2)设转动的半径为r,设绳子与水平方向的夹角为α,根据几何关系有:${r}^{2}+{L}^{2}=(\sqrt{3}L-r)^{2}$,
解得r=$\frac{\sqrt{3}}{3}L$.
cosα=$\frac{r}{\sqrt{3}L-r}=\frac{1}{2}$,即α=60°,
对小球进行受力分析,
在竖直方向上有:Tsinα=mg
在水平方向上有:T+Tcosα=mω2r
联立解得T=$\frac{2\sqrt{3}}{3}mg$,ω=$\sqrt{\frac{3g}{L}}$.
(3)轻绳断掉时,小圆环的线速度v=$rω=\frac{\sqrt{3}}{3}L•\sqrt{\frac{3g}{L}}$=$\sqrt{gL}$,
根据H=$\frac{1}{2}g{t}^{2}$得,t=$\sqrt{\frac{2H}{g}}=\sqrt{\frac{2×\frac{3L}{2}}{g}}=\sqrt{\frac{3L}{g}}$,
则平抛运动的水平位移x=$vt=\sqrt{gL}•\sqrt{\frac{3L}{g}}=\sqrt{3}L$,
根据几何关系知,R=$\sqrt{{x}^{2}+{r}^{2}}=\sqrt{3{L}^{2}+\frac{1}{3}{L}^{2}}=\frac{\sqrt{30}}{3}L$.
即环落在以杆为圆心,半径为$\frac{\sqrt{30}}{3}L$的圆周上.
答:(1)此时轻绳的张力T大小为$\frac{2\sqrt{3}}{3}mg$.
(2)竖直棒转动的角速度为$\sqrt{\frac{3g}{L}}$.
(3)环落在水平地面上的区域范围为以杆为圆心,半径为$\frac{\sqrt{30}}{3}L$的圆周上.
点评 本题考查了圆周运动和平抛运动的综合运用,知道平抛运动在水平方向和竖直方向上的运动规律以及圆周运动向心力的来源是解决本题的关键.

| A. | E0 | B. | $\frac{m}{m′}$E0 | C. | $\frac{m}{m′-m}$E0 | D. | $\frac{m′m}{(m′-m)^{2}}$E0 |
| A. | 物体的两个分运动是直线运动,则它们的合运动一定是直线运动 | |
| B. | 合运动与分运动互不影响 | |
| C. | 合运动运动了3s,分运动可能运动了3.5s | |
| D. | 合运动的速度的大小一定大于分运动速度的大小 |
| A. | 每根弹簧产生的弹力为150N | |
| B. | 人的每只手受到拉力器的拉力为300N | |
| C. | 每根弹簧的劲度系数为125N/m | |
| D. | 每根弹簧的劲度系数为500N/m |
 如图所示为一组未知方向的匀强电场的电场线,将带电荷量为q=-1.0×10-6C的点电荷由A点沿水平线移至B点,克服静电力做了2×10-6J的功,已知A、B间的距离为2cm.
如图所示为一组未知方向的匀强电场的电场线,将带电荷量为q=-1.0×10-6C的点电荷由A点沿水平线移至B点,克服静电力做了2×10-6J的功,已知A、B间的距离为2cm.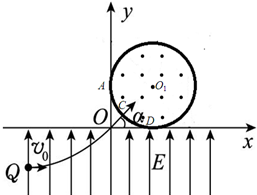 如图所示,在平面直角坐标系xOy内,第Ⅰ象限的半径R=h的圆形区域内存在垂直于坐标平面向外的匀强磁场,圆与x、y坐标轴切于D、A两点,y<0的区域内存在着沿y轴正方向的匀强电场.一质量为m、电荷量为q的带正电粒子从电场中Q(-2h,-h)点以速度v0水平向右射出,从坐标原点O射入第Ⅰ象限,与水平方向夹角为α,经磁场能以垂直于x轴的方向从D点射入电场.不计粒子的重力,求:
如图所示,在平面直角坐标系xOy内,第Ⅰ象限的半径R=h的圆形区域内存在垂直于坐标平面向外的匀强磁场,圆与x、y坐标轴切于D、A两点,y<0的区域内存在着沿y轴正方向的匀强电场.一质量为m、电荷量为q的带正电粒子从电场中Q(-2h,-h)点以速度v0水平向右射出,从坐标原点O射入第Ⅰ象限,与水平方向夹角为α,经磁场能以垂直于x轴的方向从D点射入电场.不计粒子的重力,求: 如图所示,光滑导热活塞C将体积为V0的导热容器分成A、B两室,A、B中各封有一定质量的同种气体,A室左侧连接有一U形气压计(U形管内气体的体积忽略不计),B室右侧有一阀门K,可与外界大气相通,外界大气压等于76cmHg,气温恒定.当光滑导热活塞C静止时,A、B两室容积相等,气压计水银柱高度差为38cm.现将阀门K打开,当活塞C不再移动时,求:
如图所示,光滑导热活塞C将体积为V0的导热容器分成A、B两室,A、B中各封有一定质量的同种气体,A室左侧连接有一U形气压计(U形管内气体的体积忽略不计),B室右侧有一阀门K,可与外界大气相通,外界大气压等于76cmHg,气温恒定.当光滑导热活塞C静止时,A、B两室容积相等,气压计水银柱高度差为38cm.现将阀门K打开,当活塞C不再移动时,求: 如图所示,在同一竖直平面内,A、B为光滑水平轨道的两端点,其左端A固定一挡板,轻质弹簧的左端固定在挡板上,另一自由端被质量为m的小球压在P点处.CD是以B为圆心、半径为R的$\frac{1}{4}$圆弧轨道,ABD在同一直线上.将小球释放后,小球离开B点后落在圆弧轨道上的N点.已知小球到达B点前已与弹簧分离,BN与BD间的夹角θ=30°,不计空气阻力,重力加速度为g,求:
如图所示,在同一竖直平面内,A、B为光滑水平轨道的两端点,其左端A固定一挡板,轻质弹簧的左端固定在挡板上,另一自由端被质量为m的小球压在P点处.CD是以B为圆心、半径为R的$\frac{1}{4}$圆弧轨道,ABD在同一直线上.将小球释放后,小球离开B点后落在圆弧轨道上的N点.已知小球到达B点前已与弹簧分离,BN与BD间的夹角θ=30°,不计空气阻力,重力加速度为g,求: