题目内容
19．
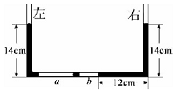如图，粗细均匀的U型玻璃管两端开口，底部的水平管内有长度分别为10cm、5cm的两段空气柱a、b，左右两管竖直，水银柱的长度如图中标注所示，在左管内缓慢注入一定量的水银，稳定后右管的水银面比原来高h=10cm，已知大气压强P0=76cmHg，环境稳定恒定，求向左管注入的水银柱长度．
分析 根据玻意耳定律求出注入水银后两部分气体的长度，再结合几何关系即可求解向左管注入的水银柱长度；
解答 解：初状态a、b两部分空气柱的压强：P1═76cmHg+14cmHg=90cmHg
因右管水银面升高的高度10cm＜12cm，故b空气柱仍在水平直管内．
末状态a、b两部分空气柱的压强：P2=76cmHg+14cmHg+10cmHg=100cmHg
设末状态a、b两部分空气柱的长度分别为La2、Lb2：
对a部分空气柱，根据波意耳定律：P1La1S=P2La2S
对b部分空气柱，根据波意耳定律：P1Lb1S=P2Lb2S
代入数据解得：La2=9cm，Lb2=4.5cm
左管所注入的水银柱长度：L=2h+（La1+Lb1）-（La2+Lb2）
代入数据解得：L=21.5cm
答：向左管注入的水银柱长度为21.5cm．
点评 本题考查气体定律的综合运用，解题关键是判断末状态时b空气柱仍在水平直管中，分析两部分气体的状态参量，气体发生等温变化，由玻意耳定律求解即可．
练习册系列答案
相关题目
如图所示，在坐标系xoy的第一象限内存在一匀强磁场B1（大小未知），磁场方向垂直于xoy平面向里；第四象限内有沿y轴正方向的匀强电场，电场强度大小为E，一带电量为+q、质量为m的粒子，自y轴的P点沿x轴正方向射入第四象限，经x轴上的Q点进入第一象限，已知OP=d，OM=OQ=2d，不计粒子重力．
10．水的流速随离岸的距离的变化关系如图甲所示，船在静水中的速度与时间的关系如图乙所示，若要使船以最短时间渡河，则（ ）
| A． | 船渡河的最短时间是60s | |
| B． | 船在行驶过程中，船的合位移垂直河岸 | |
| C． | 船在河水中航行的轨迹是一条直线 | |
| D． | 船在河水中的最大速度是5m/s |
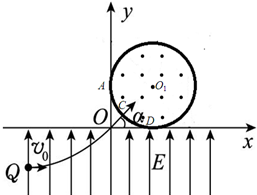如图所示，在平面直角坐标系xOy内，第Ⅰ象限的半径R=h的圆形区域内存在垂直于坐标平面向外的匀强磁场，圆与x、y坐标轴切于D、A两点，y＜0的区域内存在着沿y轴正方向的匀强电场．一质量为m、电荷量为q的带正电粒子从电场中Q（-2h，-h）点以速度v0水平向右射出，从坐标原点O射入第Ⅰ象限，与水平方向夹角为α，经磁场能以垂直于x轴的方向从D点射入电场．不计粒子的重力，求：
如图所示，一导热性能良好、内壁光滑的气缸竖直放置，在距气缸底部L=36cm处有一与气缸固定连接的卡环，活塞与气缸底部之间封闭了一定质量的气体．当气体的温度T0=300K、大气压强P0=1.0×105Pa时，活塞与汽缸底部之间的距离L0=30cm，不计活塞的重量和厚度．现对气缸加热，使活塞缓慢上升，求：
如图所示，光滑导热活塞C将体积为V0的导热容器分成A、B两室，A、B中各封有一定质量的同种气体，A室左侧连接有一U形气压计（U形管内气体的体积忽略不计），B室右侧有一阀门K，可与外界大气相通，外界大气压等于76cmHg，气温恒定．当光滑导热活塞C静止时，A、B两室容积相等，气压计水银柱高度差为38cm．现将阀门K打开，当活塞C不再移动时，求：
8．对于两个分运动的合运动，下列说法中正确的是（ ）
| A． | 物体的两个分运动是直线运动，则它们的合运动一定是直线运动 | |
| B． | 合运动与分运动互不影响 | |
| C． | 合运动运动了3s，分运动可能运动了3.5s | |
| D． | 合运动的速度的大小一定大于分运动速度的大小 |
9．
如图所示，质量相同的木块A，B用轻质弹簧连接静止在光滑的水平面上，弹簧处于自然状态．现用水平恒力F推A，则从开始到弹簧第一次被压缩到最短的过程中，（ ）
如图所示，质量相同的木块A，B用轻质弹簧连接静止在光滑的水平面上，弹簧处于自然状态．现用水平恒力F推A，则从开始到弹簧第一次被压缩到最短的过程中，（ ）| A． | 两木块速度相同时，加速度a A=a B | B． | 两木块速度相同时，加速度a A＜a B | ||
| C． | 两木块加速度相同时，速度v A＜v B | D． | 两木块加速度相同时，速度v A＞v B |