题目内容
16.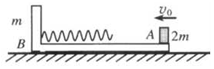 如图所示,在光滑的水平面上静止放一质量为m的“L”型木板B,木板表面光滑,左端固定一轻质弹簧,质量为2m的木块A以速度v0从板的右端水平向左滑上木板B,在木块A与弹簧相互作用的过程中,下列判断正确的是( )
如图所示,在光滑的水平面上静止放一质量为m的“L”型木板B,木板表面光滑,左端固定一轻质弹簧,质量为2m的木块A以速度v0从板的右端水平向左滑上木板B,在木块A与弹簧相互作用的过程中,下列判断正确的是( )| A. | 弹簧压缩量最大时,B板运动速率最大 | |
| B. | B板的加速度一直增大 | |
| C. | 弹簧给木块A的冲量大小为$\frac{4}{3}$mv0 | |
| D. | 弹簧的最大弹性势能为$\frac{1}{3}$mv02 |
分析 在木块A与弹簧相互作用的过程中,根据B板的受力情况分析其速度变化情况,由牛顿第二定律分析其加速度的变化情况.根据系统的动量守恒,机械能也守恒列出两个方程后联立求出A离开弹簧时的速度,再由动量定理求弹簧对A的冲量大小.当滑块与长木板速度相等时,弹簧的压缩量最大,由两大守恒定律求解弹簧的最大弹性势能.
解答 解:A、在木块A与弹簧相互作用的过程中,从弹簧的压缩量达到最大到弹簧恢复原状的过程中,弹簧对木板B有向左的弹力,B板仍在加速,所以弹簧压缩量最大时,B板运动速率不是最大,当弹簧恢复原长时B板的速率最大,故A错误;
B、弹簧压缩量先增加后减小,弹簧对B板的弹力先增大后减小,故B板的加速度先增加后减小,故B错误;
C、设弹簧恢复原长时A与B的速度分别为v1和v2.
取向左为正方向,根据动量守恒定律,有:2mv0=2mv1+mv2 ①
根据机械能守恒定律,有:$\frac{1}{2}$•2m•v02=$\frac{1}{2}$•2m•v12+$\frac{1}{2}$mv22 ②
解得:v1=$\frac{1}{3}$v0,v2=$\frac{4}{3}$v0.
对滑块A,根据动量定理,有:I=2mv1-2mv0=-$\frac{4}{3}$mv0(负号表示方向向右),故C正确;
D、当滑块与长木板速度相等时,弹簧的压缩量最大;
根据动量守恒定律,有:2mv0=(m+2m)v ③
系统机械能守恒,根据守恒定律,有:Ep=$\frac{1}{2}$•2m•v02-$\frac{1}{2}$(2m+m)v2 ④
由③④两式解得:Ep=$\frac{1}{3}$mv02,故D正确;
故选:CD
点评 本题的关键是要明确系统的运动规律,然后多次运用动量守恒定律和机械能守恒定律列式求解.

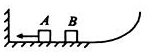 如图所示,光滑水平轨道的左边与墙壁对接,右边与一个半径为0.5m的$\frac{1}{4}$光滑竖直圆弧轨道平滑相连,物块A、B(均可视为质点)静置于光滑水平轨道上.现让物块A以6m/s的速度水平向左运动与墙壁相碰,碰撞的时间为0.01s,碰后瞬间的速度大小为5m/s.当物块A与物块B碰撞后立即粘在一起运动.已知物块A的质量为1.0kg,物块B的质量为l.5kg,g取l0m/s2.则( )
如图所示,光滑水平轨道的左边与墙壁对接,右边与一个半径为0.5m的$\frac{1}{4}$光滑竖直圆弧轨道平滑相连,物块A、B(均可视为质点)静置于光滑水平轨道上.现让物块A以6m/s的速度水平向左运动与墙壁相碰,碰撞的时间为0.01s,碰后瞬间的速度大小为5m/s.当物块A与物块B碰撞后立即粘在一起运动.已知物块A的质量为1.0kg,物块B的质量为l.5kg,g取l0m/s2.则( )| A. | 物块A、B碰撞后瞬间的速度v=2m/s | |
| B. | 物块A、B滑上圆弧轨道的最大高度h=0.05m | |
| C. | 物块A与墙壁、物块A与B碰撞过程中,系统损失的动能之比为11:15 | |
| D. | 物块A与墙壁碰撞的过程中,墙壁对A的平均作用力的大小F=100N |
| A. | 介质的折射率是$\frac{1}{\sqrt{2}}$ | |
| B. | 这束光在介质中传播的速度是1.5×108m/s | |
| C. | 这束光的频率是5×1014Hz | |
| D. | 这束光发生全反射的临界角是30° |
 一个圆盘在水平面内匀速转动,角速度是4rad/s.盘面上距圆盘中心0.10m的位置有一个质量为0.10kg的小物体在随圆盘一起做匀速圆周运动,如图所示
一个圆盘在水平面内匀速转动,角速度是4rad/s.盘面上距圆盘中心0.10m的位置有一个质量为0.10kg的小物体在随圆盘一起做匀速圆周运动,如图所示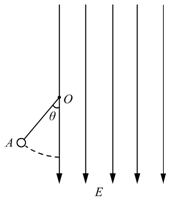 如图所示,质量m=1.0kg、带电量q=-4×10-3C的小球用长度l=0.8m的不可伸长的绝缘轻质细线悬吊在O点,过O点的竖直线右侧有竖直向下足够大的匀强电场,场强大小E=5×103N/C.现将小球拉至A处,此时,细线与竖直方向成θ角.现由静止释放小球,在小球运动过程中细线始终未被拉断.已知cosθ=$\frac{3}{4}$,取重力加速度g=10m/s2.
如图所示,质量m=1.0kg、带电量q=-4×10-3C的小球用长度l=0.8m的不可伸长的绝缘轻质细线悬吊在O点,过O点的竖直线右侧有竖直向下足够大的匀强电场,场强大小E=5×103N/C.现将小球拉至A处,此时,细线与竖直方向成θ角.现由静止释放小球,在小球运动过程中细线始终未被拉断.已知cosθ=$\frac{3}{4}$,取重力加速度g=10m/s2.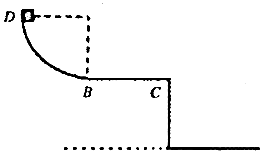 如图所示,半径为R的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B 与长为L的水平桌面相切于B点,BC离地面高为h,可视为质点的质量为m的滑块从圆 弧顶点D由静止释放,已知滑块与水平桌面间的动摩擦因数μ,重力加速度为g,求:
如图所示,半径为R的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B 与长为L的水平桌面相切于B点,BC离地面高为h,可视为质点的质量为m的滑块从圆 弧顶点D由静止释放,已知滑块与水平桌面间的动摩擦因数μ,重力加速度为g,求: 如图所示,质量为M=0.5g的木板静止在光滑水平面上,质量为m=0.245kg的物块(可视为质点)放在的木板左端,物块与木板间的动摩擦因数为μ=0.4,质量m0=0.005kg的子弹以速度v0=300m/s沿水平方向射入物块并留在其中,木块足够长,g取10m/s2.求:
如图所示,质量为M=0.5g的木板静止在光滑水平面上,质量为m=0.245kg的物块(可视为质点)放在的木板左端,物块与木板间的动摩擦因数为μ=0.4,质量m0=0.005kg的子弹以速度v0=300m/s沿水平方向射入物块并留在其中,木块足够长,g取10m/s2.求: