题目内容
8.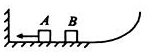 如图所示,光滑水平轨道的左边与墙壁对接,右边与一个半径为0.5m的$\frac{1}{4}$光滑竖直圆弧轨道平滑相连,物块A、B(均可视为质点)静置于光滑水平轨道上.现让物块A以6m/s的速度水平向左运动与墙壁相碰,碰撞的时间为0.01s,碰后瞬间的速度大小为5m/s.当物块A与物块B碰撞后立即粘在一起运动.已知物块A的质量为1.0kg,物块B的质量为l.5kg,g取l0m/s2.则( )
如图所示,光滑水平轨道的左边与墙壁对接,右边与一个半径为0.5m的$\frac{1}{4}$光滑竖直圆弧轨道平滑相连,物块A、B(均可视为质点)静置于光滑水平轨道上.现让物块A以6m/s的速度水平向左运动与墙壁相碰,碰撞的时间为0.01s,碰后瞬间的速度大小为5m/s.当物块A与物块B碰撞后立即粘在一起运动.已知物块A的质量为1.0kg,物块B的质量为l.5kg,g取l0m/s2.则( )| A. | 物块A、B碰撞后瞬间的速度v=2m/s | |
| B. | 物块A、B滑上圆弧轨道的最大高度h=0.05m | |
| C. | 物块A与墙壁、物块A与B碰撞过程中,系统损失的动能之比为11:15 | |
| D. | 物块A与墙壁碰撞的过程中,墙壁对A的平均作用力的大小F=100N |
分析 对于A对碰撞墙壁的过程,应用动量定理可以求出墙壁对A的平均作用力.根据初末速度求出系统损失的动能.
对于A、B碰撞过程,根据系统动量守恒求出碰后两者的共同速度,由能量守恒定律求系统损失的动能,之后AB一起沿圆弧轨道上升,由机械能守恒定律可以求出上滑的最大高度.
解答 解:A、设碰撞后A、B的共同速度为v,以向右为正方向,由动量守恒定律得:
mAv′1=(mA+mB)v
得:v=$\frac{{m}_{A}v{′}_{1}}{{m}_{A}+{m}_{B}}$=$\frac{1×5}{1+1.5}$=2m/s.故A正确.
B、A、B在光滑圆形轨道上滑动时,只有重力做功,其机械能守恒,由机械能守恒定律得:$\frac{1}{2}$(mA+mB)v2=(mA+mB)gh,
代入数据解得:h=0.2m.故B错误.
C、在物块A与墙壁中,系统损失的动能为△Ek1=$\frac{1}{2}{m}_{A}{v}_{1}^{2}$-$\frac{1}{2}{m}_{A}{v}_{1}^{′2}$=$\frac{1}{2}$×1×(62-52)J=5.5J
在物块A与B碰撞过程中,系统损失的动能为△Ek2=$\frac{1}{2}{m}_{A}{v}_{1}^{′2}$-$\frac{1}{2}$(mA+mB)v2=$\frac{1}{2}$×1×52-$\frac{1}{2}×2.5×{2}^{2}$=7.5J
故△Ek1:△Ek2=11:15,故C正确.
D、物块A与墙壁碰撞的过程中,设水平向右为正方向,对A,由动量定理得:Ft=mAv′1-mA•(-v1)
得墙壁对A的平均作用力为:F=$\frac{{m}_{A}(v{′}_{1}+{v}_{1})}{t}$=$\frac{1×(5+6)}{0.01}$N=110N.故D错误.
故选:AC
点评 分析清楚物体的运动过程,把握每个过程所遵守的物理规律是关键.要知道对于碰撞的过程,往往根据动量定理求作用力.

 名校课堂系列答案
名校课堂系列答案| A. | 鸡蛋与水泥地面接触的过程中动量变化较大 | |
| B. | 两次接触的过程中鸡蛋的动量变化相同 | |
| C. | 鸡蛋和海绵垫子接触的过程中动量变化较大 | |
| D. | 落在海绵垫子上鸡蛋所受合外力的冲量较大 |
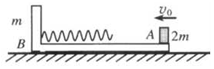 如图所示,在光滑的水平面上静止放一质量为m的“L”型木板B,木板表面光滑,左端固定一轻质弹簧,质量为2m的木块A以速度v0从板的右端水平向左滑上木板B,在木块A与弹簧相互作用的过程中,下列判断正确的是( )
如图所示,在光滑的水平面上静止放一质量为m的“L”型木板B,木板表面光滑,左端固定一轻质弹簧,质量为2m的木块A以速度v0从板的右端水平向左滑上木板B,在木块A与弹簧相互作用的过程中,下列判断正确的是( )| A. | 弹簧压缩量最大时,B板运动速率最大 | |
| B. | B板的加速度一直增大 | |
| C. | 弹簧给木块A的冲量大小为$\frac{4}{3}$mv0 | |
| D. | 弹簧的最大弹性势能为$\frac{1}{3}$mv02 |
| A. | 三个小球的加速度相同 | |
| B. | 三个小球所受的重力做功不同 | |
| C. | 三个小球所受的重力平均功率相同 | |
| D. | 斜向上抛出的小球能达到的高度最大 |
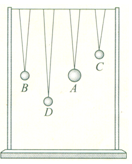 如图所示,在一条张紧的绳子上挂几个摆,其中A、B的摆长相等.先让A摆振动起来,其它各摆随后也跟着做受迫振动.稳定后,( )
如图所示,在一条张紧的绳子上挂几个摆,其中A、B的摆长相等.先让A摆振动起来,其它各摆随后也跟着做受迫振动.稳定后,( )| A. | B、C、D摆的振动周期不同 | B. | B、C、D摆的振动周期相同 | ||
| C. | D摆振幅最大 | D. | C摆振幅最大 |
| A. | 若两车的初动量相同,质量大的滑行时间长 | |
| B. | 若两车的初动能相同,质量大的滑行时间长 | |
| C. | 若两车质量相同,动量大的滑行时间长 | |
| D. | 若两车质量相同,动能大的滑行时间长 |
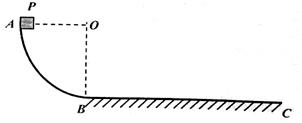 如图所示,竖直放置的光滑四分之-圆弧形轨道与足够长的粗糙水平轨道BC平滑连接.现将一质量m=1kg的滑块P(滑块的尺寸忽略不计)由A点静止释放,使其沿圆弧轨道下滑至B点,然后沿水平轨道继续向前滑行,最终停在水平轨道上的C点. 已知圆弧形轨道的半径R=0.8m,滑块与水平轨道间的动摩擦因数μ=0.1,求:
如图所示,竖直放置的光滑四分之-圆弧形轨道与足够长的粗糙水平轨道BC平滑连接.现将一质量m=1kg的滑块P(滑块的尺寸忽略不计)由A点静止释放,使其沿圆弧轨道下滑至B点,然后沿水平轨道继续向前滑行,最终停在水平轨道上的C点. 已知圆弧形轨道的半径R=0.8m,滑块与水平轨道间的动摩擦因数μ=0.1,求: 图示为某园林中使用的自动喷灌设备,每个喷头离地1.5m,都沿水平方向,向四周喷水,喷水速度在0-3m/s之间自由变化.空气阻力忽略不计,g取10m/s2.求:
图示为某园林中使用的自动喷灌设备,每个喷头离地1.5m,都沿水平方向,向四周喷水,喷水速度在0-3m/s之间自由变化.空气阻力忽略不计,g取10m/s2.求: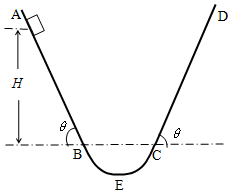 如图所示,AB(光滑)与CD(粗糙)为两个对称斜面,斜面的倾角均为θ,其上部都足够长,下部分别与一个光滑的圆弧面BEC的两端相切,一个物体在离切点B的高度为H处,以初速度v0沿斜面向下运动,物体与CD斜面的动摩擦因数为μ.
如图所示,AB(光滑)与CD(粗糙)为两个对称斜面,斜面的倾角均为θ,其上部都足够长,下部分别与一个光滑的圆弧面BEC的两端相切,一个物体在离切点B的高度为H处,以初速度v0沿斜面向下运动,物体与CD斜面的动摩擦因数为μ.