题目内容
6.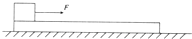 如图所示,质量为M、长度为L的木板静止在光滑的水平面上,质量为m的小物块(可视为质点)放在木板的最左端,现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动,物块和木板之间的滑动摩擦力为f,物块滑到木板的最右端时,木板运动的距离为x,在这个过程中,以下结论正确的是( )
如图所示,质量为M、长度为L的木板静止在光滑的水平面上,质量为m的小物块(可视为质点)放在木板的最左端,现用一水平恒力F作用在小物块上,使物块从静止开始做匀加速直线运动,物块和木板之间的滑动摩擦力为f,物块滑到木板的最右端时,木板运动的距离为x,在这个过程中,以下结论正确的是( )| A. | 恒力F所做的功为FL | |
| B. | 物块到达木板最右端时,木板具有的动能为fL | |
| C. | 物块的动能增加(F-f)(x+L) | |
| D. | 拉力做的功等于物块和木板机械能的增加量以及它们产生的热量之和 |
分析 根据功的公式W=Fl,分别求出恒力F和摩擦力对物块做的功.对木板和物块分别运用动能定理可求得它们动能的增加量.整个过程中物块和小车增加的机械能为F(x+L)-fL.整个过程物块和小车间摩擦生热等于系统克服摩擦力做功.
解答 解:A、物块相对地面的位移为x+L,则恒力F所做的功为F(x+L),故A错误.
B、物块到达木板最右端时,对木板,由动能定理得:木板的动能 Ek板=fx,故B错误.
C、对物块,由动能定理得:木块的动能 Ek块=(F-f)(x+L),故C正确.
D、根据功能关系知,拉力做的功等于物块和木板机械能的增加量以及它们产生的热量之和.故D正确.
故选:CD
点评 本题考查对功与能的关系的理解能力,要抓住恒力F和摩擦力f对单个物体做功应根据对地位移求,摩擦生热根据相对位移求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
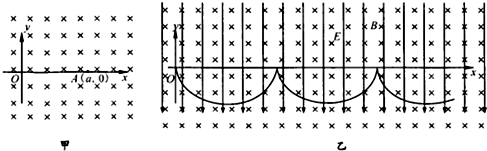
9.如图所示,甲、乙两物体分别从A点和B点同时由静止开始做匀加速直线运动,结果二者同时到达C点,D是C点右侧一点,下面说法中正确的是( )


| A. | 两物体在到达C点前乙的速度先大于甲后小于甲 | |
| B. | 两物体在到达C点前的任一位置,总有甲的速度大于乙的速度 | |
| C. | 甲在BC间的平均速度可能小于乙的平均速度 | |
| D. | 欲使两物体由静止开始运动同时到达D点,且保持各自的加速度不变,则需要甲先运动 |
7.假设地球是一半径为R,质量分布均匀的球体.已知质量分布均匀的球壳对壳内物体引力为零,有人设想要打穿地球从中国建立一条通过地心的孔径大小可忽略的光滑隧道直达巴西.如只考虑物体间的万有引力,则从隧道口抛下一物体,物体的加速度( )
| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
1.交流发电机在工作时电动势为e=Emsin2ωt,若将发电机的转速提高一倍,同时将电枢所围面积减小一半,匝数增加一倍,磁感应强度增加一倍,其他条件不变,则电动势为( )
| A. | e′=Emsin$\frac{ωt}{2}$ | B. | e′=2Emsin$\frac{ωt}{2}$ | C. | e′=2Emsin2ωt | D. | e′=4Emsin4ωt |
18.某人用弹簧秤在北极的地面称量质量为m的物体时,示数是F1;若在北极上空距地面高h处称量,示数为F2,若在赤道表面称量,示数为F3;若在地球同步卫星中称量,示数为F4;已知地球的质量为M,地球的为半径为R,自转周期为T,万有引力常量为G,下列说法正确的是( )
| A. | F1=$\frac{GMm}{{R}^{2}}$ | B. | F2=$\frac{R}{R-h}$F1 | C. | F2=F1-m$\frac{{4π}^{2}}{{T}^{2}}$R | D. | F1=m$\frac{{4π}^{2}}{{T}^{2}}$R |
16. 如图所示,质量为m的木块在质量为M的长木板上向右滑行,木块同时受到水平向右的力F作用,长木板处于静止状态.已知木块和长木板之间的动摩擦因数为μ1,木板与地面之间的动摩擦因数为μ2,下列说法正确的是( )
如图所示,质量为m的木块在质量为M的长木板上向右滑行,木块同时受到水平向右的力F作用,长木板处于静止状态.已知木块和长木板之间的动摩擦因数为μ1,木板与地面之间的动摩擦因数为μ2,下列说法正确的是( )
 如图所示,质量为m的木块在质量为M的长木板上向右滑行,木块同时受到水平向右的力F作用,长木板处于静止状态.已知木块和长木板之间的动摩擦因数为μ1,木板与地面之间的动摩擦因数为μ2,下列说法正确的是( )
如图所示,质量为m的木块在质量为M的长木板上向右滑行,木块同时受到水平向右的力F作用,长木板处于静止状态.已知木块和长木板之间的动摩擦因数为μ1,木板与地面之间的动摩擦因数为μ2,下列说法正确的是( )| A. | 木板受到的摩擦力可能是μ1mg | |
| B. | 木块受到摩擦力一定是μ1mg | |
| C. | 当F>μ2(m+M)g时,木板与木块之间发生相对运动 | |
| D. | 无论怎样改变F的大小,木板都不会运动 |
 同学采用蹲踞式起跑,在发令枪响后,左脚迅速蹬离起跑器,在向前加速的同时提升身体重心.如图,假设他的质量为m,在起跑后前进的距离s内,重心上升高度为h,获得的速度为v,阻力做功为W阻,则在此过程中:
同学采用蹲踞式起跑,在发令枪响后,左脚迅速蹬离起跑器,在向前加速的同时提升身体重心.如图,假设他的质量为m,在起跑后前进的距离s内,重心上升高度为h,获得的速度为v,阻力做功为W阻,则在此过程中: