题目内容
20.2015年9月14日12时42分,我国在酒泉卫星发射中心成功将高分九号送入太空,高分九号卫星是国家高分辨率对地观测系统科技重大专项安排的一颗光学遥感卫星,地面像元分辨率最高可达亚米级.若卫星进入运行轨道后,将卫星的运行轨道看做圆轨道,其运行周期为T,距地面的高度为h,已知地球半径为R,引力常量为G,则( )| A. | 卫星运动的加速度为$\frac{4{π}^{2}R}{{T}^{2}}$ | |
| B. | 地球第一宇宙速度为$\frac{2π(R+h)}{T}$$\sqrt{\frac{R+h}{R}}$ | |
| C. | 地球表面的重力加速度为$\frac{4{π}^{2}(R+h)^{3}}{R{T}^{2}}$ | |
| D. | 地球的平均密度为$\frac{3π(R+h)^{3}}{G{T}^{2}{R}^{3}}$ |
分析 根据向心加速度与周期的关系求出卫星的加速度,根据万有引力提供向心力,求出地球的第一宇宙速度,结合万有引力等于重力求出地球表面的重力加速度,根据地球的质量以及地球的体积求出平均密度.
解答 解:A、卫星的加速度a=$(R+h)\frac{4{π}^{2}}{{T}^{2}}$,故A错误.
B、根据$G\frac{Mm}{(R+h)^{2}}=m(R+h)\frac{4{π}^{2}}{{T}^{2}}$得,GM=$\frac{4{π}^{2}(R+h)^{3}}{{T}^{2}}$,根据$G\frac{Mm}{{R}^{2}}=m\frac{{v}^{2}}{R}$得,第一宇宙速度v=$\sqrt{\frac{GM}{R}}$=$\frac{2π(R+h)}{T}\sqrt{\frac{R+h}{R}}$,故B正确.
C、地球表面的重力加速度g=$\frac{GM}{{R}^{2}}=\frac{4{π}^{2}(R+h)^{3}}{{R}^{2}{T}^{2}}$,故C错误.
D、地球的平均密度$ρ=\frac{M}{\frac{4π{R}^{3}}{3}}=\frac{3π(R+h)^{3}}{G{T}^{2}{R}^{3}}$,故D正确.
故选:BD.
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
11.如图为一物体沿直线运动的速度图象,由此可知( )


| A. | 2s末物体返回出发点 | |
| B. | 4s末物体运动方向改变 | |
| C. | 3s末与5s末的速度大小相等,方向相反 | |
| D. | 8s末物体返回出发点 |
15.钢球A自塔顶自由落下2m时,钢球B自离塔顶6m距离处自由落下,两钢球同时到达地面,不计空气阻力,则塔高为( )
| A. | 24m | B. | 16m | C. | 12m | D. | 8m |
5.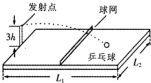 一带有乒乓球发射机的乒乓球台如图所示.水平台面的长和宽分别为L1和L2,中间球网高度为h.发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h,不考虑乒乓球的旋转和空气阻力(重力加速度为g),则( )
一带有乒乓球发射机的乒乓球台如图所示.水平台面的长和宽分别为L1和L2,中间球网高度为h.发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h,不考虑乒乓球的旋转和空气阻力(重力加速度为g),则( )
 一带有乒乓球发射机的乒乓球台如图所示.水平台面的长和宽分别为L1和L2,中间球网高度为h.发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h,不考虑乒乓球的旋转和空气阻力(重力加速度为g),则( )
一带有乒乓球发射机的乒乓球台如图所示.水平台面的长和宽分别为L1和L2,中间球网高度为h.发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h,不考虑乒乓球的旋转和空气阻力(重力加速度为g),则( )| A. | 若球发射速度v=$\frac{{L}_{1}}{8}$$\sqrt{\frac{g}{h}}$,则恰好越过球网落在球台的右侧 | |
| B. | 若球发射速度v=$\frac{{L}_{2}}{4}$$\sqrt{\frac{g}{h}}$,则恰好越过球网落在球台的右侧 | |
| C. | 若球发射速度v=L2$\sqrt{\frac{g}{6h}}$,则恰好落在球台的右侧边缘 | |
| D. | 若球以速度v=L1$\sqrt{\frac{g}{6h}}$垂直台面左侧底线水平发射,则恰好落在球台的右侧边缘 |
9.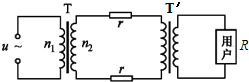 图为远距离输电示意图,两变压器均为理想变压器,升压变压器T的原、副线圈匝数比为k1.降压变压器T′的原、副线圈匝数比k2.原线圈两端接入一电压u=Umsinωt的交流电源,用户电阻为R(纯电阻),若用户消耗功率为P,输电线的总电阻为2r,不考虑其它因素的影响,则输电线上损失的电功率Pr和用户获得的电压U分别为( )
图为远距离输电示意图,两变压器均为理想变压器,升压变压器T的原、副线圈匝数比为k1.降压变压器T′的原、副线圈匝数比k2.原线圈两端接入一电压u=Umsinωt的交流电源,用户电阻为R(纯电阻),若用户消耗功率为P,输电线的总电阻为2r,不考虑其它因素的影响,则输电线上损失的电功率Pr和用户获得的电压U分别为( )
 图为远距离输电示意图,两变压器均为理想变压器,升压变压器T的原、副线圈匝数比为k1.降压变压器T′的原、副线圈匝数比k2.原线圈两端接入一电压u=Umsinωt的交流电源,用户电阻为R(纯电阻),若用户消耗功率为P,输电线的总电阻为2r,不考虑其它因素的影响,则输电线上损失的电功率Pr和用户获得的电压U分别为( )
图为远距离输电示意图,两变压器均为理想变压器,升压变压器T的原、副线圈匝数比为k1.降压变压器T′的原、副线圈匝数比k2.原线圈两端接入一电压u=Umsinωt的交流电源,用户电阻为R(纯电阻),若用户消耗功率为P,输电线的总电阻为2r,不考虑其它因素的影响,则输电线上损失的电功率Pr和用户获得的电压U分别为( )| A. | Pr=$\frac{r}{Rk_2^2}$P $U=(\frac{{\sqrt{2}{k_2}{U_m}}}{{2{k_1}}})(\frac{Rk_2^2}{2r+Rk_2^2})$ | |
| B. | Pr=$\frac{2r}{Rk_2^2}$P $U=(\frac{{\sqrt{2}{U_m}}}{{2{k_1}{k_2}}})(\frac{Rk_2^2}{2r+Rk_2^2})$ | |
| C. | Pr=$\frac{2r}{Rk_2^2}$P $U=(\frac{{\sqrt{2}{k_2}{U_m}}}{{2{k_1}}})(\frac{Rk_2^2}{2r+Rk_2^2})$ | |
| D. | Pr=$\frac{2r}{Rk_1^2}$P $U=(\frac{{\sqrt{2}{U_m}}}{{2{k_1}{k_2}}})(\frac{Rk_2^2}{2r+Rk_2^2})$ |
 足够长的光滑水平面上有一质量为6kg的处于静止的木板M,停在M的右端的物块N质量为6kg,M、N间的动摩擦因数μ=0.1,用长l=0.8m的轻绳系一质量为m=1kg的小球悬挂在固定点O上,物块N与小球可视为质点,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与N发生碰撞后反弹,反弹所能达到的最大高度为h=0.2m,同时N获得1m/s的速度,不计空气阻力,g=10m/s2.求:
足够长的光滑水平面上有一质量为6kg的处于静止的木板M,停在M的右端的物块N质量为6kg,M、N间的动摩擦因数μ=0.1,用长l=0.8m的轻绳系一质量为m=1kg的小球悬挂在固定点O上,物块N与小球可视为质点,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与N发生碰撞后反弹,反弹所能达到的最大高度为h=0.2m,同时N获得1m/s的速度,不计空气阻力,g=10m/s2.求: 如图所示,质量均为M=4kg的小车A、B,B车上用轻绳挂有质量为m=2kg的小球C,与B车静止在水平地面上.A车以v0=2m/s的速度在光滑水平面上向B车运动,相碰后粘在一起(碰撞时间很短).求:
如图所示,质量均为M=4kg的小车A、B,B车上用轻绳挂有质量为m=2kg的小球C,与B车静止在水平地面上.A车以v0=2m/s的速度在光滑水平面上向B车运动,相碰后粘在一起(碰撞时间很短).求: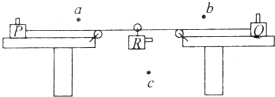 某同学利用图示装置验证系统机械能守恒定律,图中P、Q、R是三个完全相同的物块,P、Q用细绳连接,放在光滑水平桌面上,物块R与轻质滑轮连接,放在两定滑轮的中间.a、b、c是三个光电门,调整三个光电门的位置,能实现同时遮光.整个装置无初速度释放,已知P、Q、R经过三个光电门的遮光时间分别为t1、t2、t3,R的遮光片到c的距离为H,三个遮光片的宽度均为x.
某同学利用图示装置验证系统机械能守恒定律,图中P、Q、R是三个完全相同的物块,P、Q用细绳连接,放在光滑水平桌面上,物块R与轻质滑轮连接,放在两定滑轮的中间.a、b、c是三个光电门,调整三个光电门的位置,能实现同时遮光.整个装置无初速度释放,已知P、Q、R经过三个光电门的遮光时间分别为t1、t2、t3,R的遮光片到c的距离为H,三个遮光片的宽度均为x.