��Ŀ����
10����1��Ϊ���С���֤��е���غ㶨�ɡ���ʵ�飬���������Ŀɹ�ѡ��A������̨ B������ʱ�� C����дֽ D��ֽ�� E����ѹ������Դ
F����ƽ G����� H������ I������ K���׳� J���ش�
�ڸ�ʵ���У��������IJ���Ҫ����FG����ֻ����ĸ���ţ�
��2��������һʵ�飬����˵������ȷ����B��
A������Ӧѡ���ܶ�С������
B��������λ��Ӧ��ͬһ��ֱ����
C��ʵ���б������ش�������
D��Ӧ���ͷ�ֽ�������ͨ��Դ
��3��������m=1kg���ش��������䣬��ֽ���ϴ��һϵ�еĵ���ͼ1��ʾ��OΪ��һ���㣬A��B��CΪ���ڵĵ㣬���ڼ������ʱ����Ϊ0.02s�����ȵ�λ��cm��ȡg=9.8m/s2����ӵ�O�����¼�����B�Ĺ����У������������ܵļ�������Ep=0.48J�����ܵ���������Ek=0.47J�������������λ��Ч���֣���
��4��С����ʵ���У�����β������֣��ش���С���������������Դ����ش����ӵĶ��ܣ�����ڡ�����С�ڡ�������������ϵͳ�����ɵģ��ϵͳ������żȻ������
��5��С����Ϊ������������ķ�Χ�ڣ��ش��Ļ�е���غ㣮С���ã�3�������ݻ�v2-hͼ����ͼ2����ͼ�ߵ�б��Ϊk��������õ����������ٶ�Ϊ$\frac{k}{2}$��

���� �����ʵ���ʵ��ԭ������Ҫ���������ݵȣ���ȷ����ʱ����ʹ�ã�����ʵ���е�ע�������Լ���ν������ݴ����������κ�ʵ��ע���ʵ��ԭ����ʵ��������ʵ�鲽�衢ʵ�����ݴ�����ʵ��ע�������⼸��ȥ�������
����ƽ���ٶȵ�����ʱ�̵�˲ʱ�ٶȣ�������ڵ���Ƶ�ʵĵ�����������⣻
���ݻ�е���غ㶨�ɣ����v2-hͼ���б�ʺ��壬�������
��� �⣺��1����ʵ������Ҫ�̶ȳ߲���ֽ���ϵ�����ľ���Ӷ���֪���ش��½��ľ��룬�Լ�ͨ��ֽ��������ľ��룬���ƽ���ٶȣ��Ӷ���֪˲ʱ�ٶȣ�ֽ������������ʱ���ʱ������֪�����Բ���Ҫ������ش��������ɲ�ɲ��⣬
��ѡ��FG��
��2��A��Ϊ����������˶��ӽ��������壬��������������Ӧѡ���ܶȴ����С�����壻��A����
B������ֽ��ʱʹֽ��������ֱ������λ��Ӧ��ͬһ��ֱ���ϣ��Ӷ���СĦ��������B��ȷ��
C��ʵ���в�Ҫ����ش������������ʽ���߾�����������C����
D����ʼ��¼ʱ��Ӧ�ȸ�����ʱ��ͨ���㣬Ȼ�����ͷ��ش�����������ֽ��һͬ���£�����ȷſ�ֽ�����������䣬�ٽ�ͨ����ʱʱ���ĵ�Դ�����������˶��Ͽ죬���������ݵIJɼ��ʹ��������ʵ������ϴ������D����
��ѡ��B��
��3���������ܵļ�С����Ep=mgh=1��9.8��0.0486J��0.48J��
���ܵ���������Ek=$\frac{1}{2}$mvB2=$\frac{1}{2}$��1����0.97��2��0.47J��
��4��ͨ�������֪��Ep����Ek����Ϊֽ����������д���Ħ���������ã�����ϵͳ�����ɵģ�
��5�����ݻ�е���غ㶨���У�mgh=$\frac{1}{2}$mv2��
�ã�v2=2gh����v2-hͼ���ǹ�ԭ���һ��ֱ�ߣ�
ֱ�ߵ�б��k=2g����ôg=$\frac{k}{2}$��
�ʴ�Ϊ����1��FG����2��B�� ��3��0.48��0.47����4�����ڣ�ϵͳ����5��$\frac{k}{2}$��
���� ���ڻ���ʵ��Ҫ��ʵ��ԭ������ȥ���⣬Ҫ���Զ���ʵ�飬������ʵ��ľ�����������ܵ�ƾ����ȥ����ʵ�飮��ʵ����ע�����ʵ��������Դ�������ҵ����ʵķ���ȥ��С��
��������˲ʱ�ٶȵķ������������е���غ㶨�ɵ�������ע��v2-hͼ���б�ʵĺ��壮


| A�� | c�� | B�� | d�� | C�� | e�� | D�� | f�� |
 һ��������ƽֱ��·�����������������̵�v-tͼ����ͼ��ʾ������OA��Ϊֱ�ߣ�AB��Ϊ���ߣ�B���Ϊƽ���ں����ֱ�ߣ���֪��t1ʱ�̿�ʼ�����Ĺ��ʴﵽ������ұ��ֲ��䣬�����˶��������������������Ĵ�С��ΪFf������˵����ȷ���ǣ�������
һ��������ƽֱ��·�����������������̵�v-tͼ����ͼ��ʾ������OA��Ϊֱ�ߣ�AB��Ϊ���ߣ�B���Ϊƽ���ں����ֱ�ߣ���֪��t1ʱ�̿�ʼ�����Ĺ��ʴﵽ������ұ��ֲ��䣬�����˶��������������������Ĵ�С��ΪFf������˵����ȷ���ǣ�������| A�� | 0-t1ʱ���ڣ�������������˶� | B�� | 0-t2ʱ���ڣ��������ȼ����˶� | ||
| C�� | �����Ķ����P=Ffv1 | D�� | �����Ķ����P=Ffv2 |
 ��ͼ������Ϊm�Ĺ⻬С��������Ϊ����б��͵���PO֮�侲ֹ�������建��������ֱλ����ʱ��ת��ˮƽλ�õĹ����У����ڵ����С��ĵ���F1��б���С��ĵ���F2�Ĵ�С�仯����ȷ���ǣ�������
��ͼ������Ϊm�Ĺ⻬С��������Ϊ����б��͵���PO֮�侲ֹ�������建��������ֱλ����ʱ��ת��ˮƽλ�õĹ����У����ڵ����С��ĵ���F1��б���С��ĵ���F2�Ĵ�С�仯����ȷ���ǣ�������| A�� | F1���F2��С | |
| B�� | F1��С��F2��С | |
| C�� | F1����С�����F2��С | |
| D�� | F1��������С��F2��С |
 ��ͼ��ʾ��С���ˮƽλ�þ�ֹ�ͷţ���С��ͨ����͵�ʱ���ٶ�Ϊv�����ٶ�Ϊ�أ����ٶ�Ϊa����������ΪT����ô��������L��������������
��ͼ��ʾ��С���ˮƽλ�þ�ֹ�ͷţ���С��ͨ����͵�ʱ���ٶ�Ϊv�����ٶ�Ϊ�أ����ٶ�Ϊa����������ΪT����ô��������L��������������| A�� | v��a������ | B�� | �ء�a����С | C�� | T��a������ | D�� | v���ؼ�С |

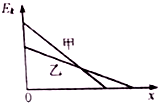
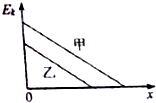
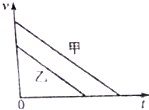 ��������ҷ��ڴֲڵ�ˮƽ���ϣ���������ͬ����ij��ٶȣ���������ڻ���Ħ�������������˶�����v-tͼ����ͼ��ʾ����֪�������������ȣ�������ȷ��ӳ������Ķ����뻬�о���x �ı仯���ɵ��ǣ�������
��������ҷ��ڴֲڵ�ˮƽ���ϣ���������ͬ����ij��ٶȣ���������ڻ���Ħ�������������˶�����v-tͼ����ͼ��ʾ����֪�������������ȣ�������ȷ��ӳ������Ķ����뻬�о���x �ı仯���ɵ��ǣ�������

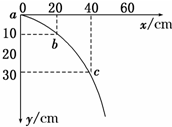 ijͬѧ����ƽ���˶�ʵ��ʱ�ó���ͼ��ʾ��С���˶��켣��a��b��c�����λ�����˶��켣���ѱ����gȡ10m/s2����
ijͬѧ����ƽ���˶�ʵ��ʱ�ó���ͼ��ʾ��С���˶��켣��a��b��c�����λ�����˶��켣���ѱ����gȡ10m/s2����