题目内容
19. 如图所示,小球从水平位置静止释放,设小球通过最低点时的速度为v,角速度为ω,加速度为a,绳的拉力为T,那么随着绳子L的增长( )
如图所示,小球从水平位置静止释放,设小球通过最低点时的速度为v,角速度为ω,加速度为a,绳的拉力为T,那么随着绳子L的增长( )| A. | v、a都增大 | B. | ω、a都减小 | C. | T、a都不变 | D. | v增大,ω减小 |
分析 小球在摆动过程中只受重力,故机械能守恒,由机械能守恒定律可求小球运动到最低点时的速度大小;
由向心力公式可求得最低点时,绳子对小球的拉力大小.
由向心加速度的表达式计算向心加速度;根据v=ωr计算角速度.
解答 解:1.由机械能守恒定律可知:
mgL=$\frac{1}{2}$mv2;
解得:v=$\sqrt{2gL}$;可知L越长,v越大
2.在最低点由向心力公式可得:
T-mg=m$\frac{{v}^{2}}{L}$;
解得:T=3mg;与L的大小无关
3.向心加速度:a=$\frac{{v}^{2}}{L}$=2g,与绳长L无关;
4.角速度:$ω=\frac{v}{L}=\sqrt{\frac{2g}{L}}$
可知绳长越长,角速度越小.
由以上的分析可知,AB错误,CD正确.
故选:CD
点评 本题考查机械能守恒定律及向心力公式,如果系统内只有重力做功,则利用机械能守恒定律可以很容易解题.

练习册系列答案
相关题目
9. 如图所示,活塞质量为m,缸套质量为M,通过弹簧吊在天花板上,气缸内封住一定质量的空气,缸套与活塞无摩擦,活塞截面积为S,大气压强为p0,则( )
如图所示,活塞质量为m,缸套质量为M,通过弹簧吊在天花板上,气缸内封住一定质量的空气,缸套与活塞无摩擦,活塞截面积为S,大气压强为p0,则( )
 如图所示,活塞质量为m,缸套质量为M,通过弹簧吊在天花板上,气缸内封住一定质量的空气,缸套与活塞无摩擦,活塞截面积为S,大气压强为p0,则( )
如图所示,活塞质量为m,缸套质量为M,通过弹簧吊在天花板上,气缸内封住一定质量的空气,缸套与活塞无摩擦,活塞截面积为S,大气压强为p0,则( )| A. | 气缸内空气的压强为p0-$\frac{Mg}{S}$ | B. | 气缸内空气的压强为p0+$\frac{mg}{S}$ | ||
| C. | 内外空气对活塞的作用力为mg | D. | 内外空气对缸套的作用力为Mg |
14.下列说法正确的是( )
| A. | 可以将工厂里扩散到外界的能量收集起来重新利用 | |
| B. | 分子间的距离增大时,分子间的引力和斥力都减小 | |
| C. | 气体对容器壁有压强是气体分子对容器壁频繁碰撞的结果 | |
| D. | 温度升高,说明物体中所有分子的动能都增大 | |
| E. | 在一个绝热容器内,不停地搅拌液体,可使液体的温度升高 |
4. 转笔包含了许多的物理知识,假设某转笔高手能让笔绕其上的某一点O做匀速圆周运动,下列有关该同学转笔中涉及到的物理知识的叙述正确的是( )
转笔包含了许多的物理知识,假设某转笔高手能让笔绕其上的某一点O做匀速圆周运动,下列有关该同学转笔中涉及到的物理知识的叙述正确的是( )
 转笔包含了许多的物理知识,假设某转笔高手能让笔绕其上的某一点O做匀速圆周运动,下列有关该同学转笔中涉及到的物理知识的叙述正确的是( )
转笔包含了许多的物理知识,假设某转笔高手能让笔绕其上的某一点O做匀速圆周运动,下列有关该同学转笔中涉及到的物理知识的叙述正确的是( )| A. | 笔杆上的点离O点越近的,做圆周运动的角速度越大 | |
| B. | 笔杆上的点离O点越近的,做圆周运动的线速度越大 | |
| C. | 笔杆做圆周运动的向心力是由万有引力提供的 | |
| D. | 若该同学使用中性笔,墨汁可能会因笔快速的转动做离心运动被甩出 |
11.下列说法正确的是( )
| A. | 第二类永动机不可能制成是因为它违反了能量守恒定律 | |
| B. | 在绝热条件下压缩理想气体,气体的内能一定增加 | |
| C. | 只要知道气体的摩尔体积和阿伏加德罗常数,就可以估算出气体分子的直径 | |
| D. | 一定质量的理想气体,压强不变、温度升高时,气体分子单位时间对气缸壁单位面积碰撞的次数将变少 |
8.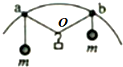 如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径,标记小物块在绳上的位置为O位置.不计所有摩擦,下列说法正确的是( )
如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径,标记小物块在绳上的位置为O位置.不计所有摩擦,下列说法正确的是( )
 如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径,标记小物块在绳上的位置为O位置.不计所有摩擦,下列说法正确的是( )
如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径,标记小物块在绳上的位置为O位置.不计所有摩擦,下列说法正确的是( )| A. | 细绳aO段与竖直方向的夹角为60° | B. | 细绳aO段与竖直方向的夹角为30° | ||
| C. | 小物块的质量为m | D. | 小物块的质量为2m |

 光滑的水平面上,一物体在F=8N的水平拉力作用下由静止开始做匀加速直线运动,2s内发生的位移为x=8m,求:
光滑的水平面上,一物体在F=8N的水平拉力作用下由静止开始做匀加速直线运动,2s内发生的位移为x=8m,求: