题目内容
16.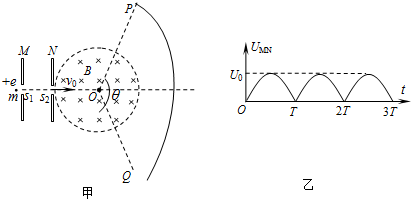 如图甲所示,两块相同的平行金属板M、N正对着放置,相距为$\frac{R}{2}$,板M、N上的小孔s1、s2与 O三点共线,s2O=R,连线s1O垂直于板M、N.以O为圆心、R为半径的圆形区域内存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场.收集屏PQ上各点到O点的距离都为2R,两端点P、Q关于连线s1O对称,屏PQ所对的圆心角θ=120°.质量为m、电荷量为e的质子连续不断地经s1进入M、N间的电场,接着通过s2进入磁场.质子重力及质子间的相互作用均不计,质子在s1处的速度看作零.
如图甲所示,两块相同的平行金属板M、N正对着放置,相距为$\frac{R}{2}$,板M、N上的小孔s1、s2与 O三点共线,s2O=R,连线s1O垂直于板M、N.以O为圆心、R为半径的圆形区域内存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场.收集屏PQ上各点到O点的距离都为2R,两端点P、Q关于连线s1O对称,屏PQ所对的圆心角θ=120°.质量为m、电荷量为e的质子连续不断地经s1进入M、N间的电场,接着通过s2进入磁场.质子重力及质子间的相互作用均不计,质子在s1处的速度看作零.(1)若M、N间的电压UMN=+U时,求质子进入磁场时速度的大小v0.
(2)若M、N间接入如图乙所示的随时间t变化的电压UMN=|U0sin$\frac{π}{T}t}$|(式中U0=$\frac{{3e{B^2}{R^2}}}{m}$,周期T已知),且在质子通过板间电场区域的极短时间内板间电场视为恒定,则质子在哪些时刻自s1处进入板间,穿出磁场后均能打到收集屏PQ上?
(3)在上述(2)问的情形下,当M、N间的电压不同时,质子从s1处到打在收集屏PQ上经历的时间t会不同,求t的最大值.
分析 (1)质子在电场中做加速运动,由动能定理可求得质子进入磁场时的速度;
(2)由动能定理可得出质子进入磁场时的速度表达式;由几何关系可知质子能打在收集屏上的临界条件,则由牛顿第二定律可求得能打在屏上的质子进入电场的时刻;
(3)根据质子在电场与磁场中运动的关系可推导出质子运动的最大时间.
解答  解:(1)根据动能定理,有:
解:(1)根据动能定理,有:
eU=$\frac{1}{2}$mv02-0
解得:v0=$\sqrt{\frac{2eU}{m}}$
(2)质子在板间运动,根据动能定理,有:
eUMN=$\frac{1}{2}$mv2-0
质子在磁场中运动,根据牛顿第二定律,有:evB=m$\frac{{v}_{\;}^{2}}{r}$
若质子能打在收集屏上,轨道半径r与半径R应满足的关系:
r≥$\sqrt{3}$R
解得板间电压:UMN≥$\frac{3e{B}_{\;}^{2}{R}_{\;}^{2}}{2m}$结合图象可知:质子在t=kT+$\frac{T}{6}$~kT+$\frac{5}{6}$T(k=0,1,2,…)之间任一时刻从s1处进入电场,均能打到收集屏上
(3)M、N间的电压越小,质子穿出电场进入磁场时的速度越小,质子在极板间经历的时间越长,同时在磁场中运动轨迹的半径越小,在磁场中运动的时间也会越长,出磁场后打到收集屏前作匀速运动的时间也越长,所以当质子打在收集屏的P端时,对应时间t最长,两板间的电压此时为:
UMN=$\frac{1}{2}$U0
在板间电场中运动时间:t1=$\frac{R}{v}$
在磁场中运动时间:t2=$\frac{60°}{360°}×\frac{2πr}{v}$=$\frac{π×\sqrt{3R}}{3v}$
出磁场后打到收集屏前作匀速运动的时间:t3=$\frac{R}{v}$所以,运动总时间为:
t=t1+t2+t3=$(\frac{2}{\sqrt{3}}+\frac{π}{3})\frac{\sqrt{3}R}{v}$=$(\frac{2}{\sqrt{3}}+\frac{π}{3})\frac{m}{eB}$;
答:(1)质子进入磁场时速度的大小为$\sqrt{\frac{2eU}{m}}$;
(2)质子在t=kT+$\frac{T}{6}$~kT+$\frac{5}{6}$T(k=0,1,2,…)之间任一时刻从s1处进入电场,均能打到收集屏上;
(3)时间t的最大值为$(\frac{2}{\sqrt{3}}+\frac{π}{3})\frac{m}{eB}$;
点评 本题要注意质子在电场中加速后进入磁场中偏转;加速电场中由动能定理求出速度,而在磁场中的运动要由几何关系确定圆心和半径,再根据牛顿第二定律及向心力公式列式求解.本题中的难点在于找出时间范围及时间的最大值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案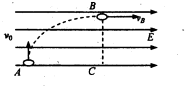 如图,一质量为m,电量+q的小球,以垂直于电场方向的速度v0竖直向上进入一个匀强电场,经过一段时间后,该小球的速度vB恰好与场强方向平行.若在此过程中水平位移是上升高度的2倍,即AC=2BC,则A、C两点间的电压是( )
如图,一质量为m,电量+q的小球,以垂直于电场方向的速度v0竖直向上进入一个匀强电场,经过一段时间后,该小球的速度vB恰好与场强方向平行.若在此过程中水平位移是上升高度的2倍,即AC=2BC,则A、C两点间的电压是( )| A. | $\frac{{mv}_{0}^2}{2q}$ | B. | $\frac{{2mv}_{0}^2}{q}$ | C. | $\frac{{mv}_{0}^2}{q}$ | D. | $\frac{{mv}_{0}^2}{4q}$ |
 如图所示,总质量为460kg的热气球,从地面刚开始竖直上升时的加速度为0.5m/s2,当热气球上升到180m 时,以5m/s的速度向上匀速运动.若离开地面后热气球所受浮力保持不变,上升过程中热气球总质量不变,重力加速度g=10m/s2.关于热气球,下列说法正确的是( )
如图所示,总质量为460kg的热气球,从地面刚开始竖直上升时的加速度为0.5m/s2,当热气球上升到180m 时,以5m/s的速度向上匀速运动.若离开地面后热气球所受浮力保持不变,上升过程中热气球总质量不变,重力加速度g=10m/s2.关于热气球,下列说法正确的是( )| A. | 所受浮力大小为4830 N | |
| B. | 加速上升过程中所受空气阻力保持不变 | |
| C. | 从地面开始上升10 s后的速度大小为5 m/s | |
| D. | 以5 m/s匀速上升时所受空气阻力大小为230 N |
| A. | 自由落体运动是匀变速运动 | |
| B. | 自由落体运动物体第一秒下落10m | |
| C. | 开始连续的三个1s内下落高度之比为1:3:5 | |
| D. | 开始连续的三个1 s末的速度之比为1:3:5 |
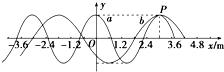 两列简谐横波a、b在同一种均匀介质中沿x轴传播,a波周期为0.5s.某时刻,两列波的波峰正好在xP=3.0m处的P点重合,如图甲所示,则b波的周期为Tb=0.8s,该时刻,离P点最近的波峰重叠点的平衡位置坐标是x=27.0或-21.0m.
两列简谐横波a、b在同一种均匀介质中沿x轴传播,a波周期为0.5s.某时刻,两列波的波峰正好在xP=3.0m处的P点重合,如图甲所示,则b波的周期为Tb=0.8s,该时刻,离P点最近的波峰重叠点的平衡位置坐标是x=27.0或-21.0m.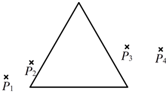 某同学测量一块玻璃三棱镜的折射率,经正确操作,插下了四枚大头针P1、P2和P3、P4,如图所示.
某同学测量一块玻璃三棱镜的折射率,经正确操作,插下了四枚大头针P1、P2和P3、P4,如图所示. 如图所示,环形区域内有垂直于纸面向外的匀强磁场,磁感应强度大小为B,内圆半径为R,外圆半径为(1+$\sqrt{2}$)R,两圆的圆心(重合)处不断向外发射电荷量为q、质量为m的带正电粒子,不计粒子所受重力及粒子间相互作用,粒子发射速度方向都水平向右,而速度大小都不同,导致一部分粒子从外圆飞出磁场,而另一部分粒子第一次出磁场是飞入内圆.
如图所示,环形区域内有垂直于纸面向外的匀强磁场,磁感应强度大小为B,内圆半径为R,外圆半径为(1+$\sqrt{2}$)R,两圆的圆心(重合)处不断向外发射电荷量为q、质量为m的带正电粒子,不计粒子所受重力及粒子间相互作用,粒子发射速度方向都水平向右,而速度大小都不同,导致一部分粒子从外圆飞出磁场,而另一部分粒子第一次出磁场是飞入内圆. 如图所示,空间区域Ⅰ、Ⅱ有匀强电场和匀强磁场,其中电场方向竖直向上,区域Ⅰ中磁场垂直纸面向内,区域Ⅱ中磁场垂直纸面向外,磁感应强度大小均为B=$\frac{mv}{qd}$,矩形区域足够长,宽为2d,在AD边中点O处有一粒子源,沿纸面向磁场中各方向均匀地辐射出速率均为v的带电粒子,该粒子进入场区后恰能作匀速圆周运动,带电粒子质量m,电荷量为q.已知重力加速度为g.
如图所示,空间区域Ⅰ、Ⅱ有匀强电场和匀强磁场,其中电场方向竖直向上,区域Ⅰ中磁场垂直纸面向内,区域Ⅱ中磁场垂直纸面向外,磁感应强度大小均为B=$\frac{mv}{qd}$,矩形区域足够长,宽为2d,在AD边中点O处有一粒子源,沿纸面向磁场中各方向均匀地辐射出速率均为v的带电粒子,该粒子进入场区后恰能作匀速圆周运动,带电粒子质量m,电荷量为q.已知重力加速度为g.