��Ŀ����
11�� ��ͼ��ʾ�������������д�ֱ��ֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB����Բ�뾶ΪR����Բ�뾶Ϊ��1+$\sqrt{2}$��R����Բ��Բ�ģ��غϣ����������ⷢ������Ϊq������Ϊm�Ĵ��������ӣ����������������������Ӽ�����ã����ӷ����ٶȷ���ˮƽ���ң����ٶȴ�С����ͬ������һ�������Ӵ���Բ�ɳ��ų�������һ�������ӵ�һ�γ��ų��Ƿ�����Բ��
��ͼ��ʾ�������������д�ֱ��ֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB����Բ�뾶ΪR����Բ�뾶Ϊ��1+$\sqrt{2}$��R����Բ��Բ�ģ��غϣ����������ⷢ������Ϊq������Ϊm�Ĵ��������ӣ����������������������Ӽ�����ã����ӷ����ٶȷ���ˮƽ���ң����ٶȴ�С����ͬ������һ�������Ӵ���Բ�ɳ��ų�������һ�������ӵ�һ�γ��ų��Ƿ�����Բ����1��������Ӵ���Բ�ɳ��ų��������ӵ��ٶȴ�С��Χ��
��2��������Ӵ���Բ�ɳ��ų�������Щ�����ڴų����˶���ʱ�䷶Χ��
��3��������ӵ�һ�γ��ų��Ƿ�����Բ������Щ���Ӵӽ���ų�����һ�γ��ų����õ�ʱ�䷶Χ��
���� ��1�������ӵĹ켣����Բ����ʱ�����ݼ��ι�ϵ����뾶�������������ṩ����������ٶ�${v}_{1}^{\;}$������Ҫ����Բ�ɳ����������ٶ�$v��{v}_{1}^{\;}$
��2���պô���Բ�ɳ�ʱ�������ڴų����˶���ʱ���������ʱ�䣬���������Щ�����ڴų����˶���ʱ�䷶Χ��
��3�����ӵ�һ�γ��ų��Ƿ�����Բ������켣Բ������Բ�ĽǷ�Χ��������ڹ�ʽ�����ɵó���Щ���Ӵӽ���ų�����һ�γ��ų����õ�ʱ�䷶Χ
��� �� ����1������������ٶȴ�С��ͬ���켣Բ�İ뾶��ͬ����պ�����Բ����ʱ���켣Բ�뾶Ϊr1����ͼ��ʾ
����1������������ٶȴ�С��ͬ���켣Բ�İ뾶��ͬ����պ�����Բ����ʱ���켣Բ�뾶Ϊr1����ͼ��ʾ
�ɼ��ι�ϵ�У���$\sqrt{2}R$+R-r1��2=R2+${r}_{1}^{2}$
�ã�r1=R
���������ṩ���������У�qv1B=m$\frac{{v}_{1}^{2}}{{r}_{1}^{\;}}$
�����ã�v1=$\frac{qBR}{m}$
������Ӵ���Բ�ɳ��������ӵ��ٶ�Ϊ��v��$\frac{qBR}{m}$
��2���������ڴų���������Բ���˶�������ΪT�����У�
T=$\frac{2��r}{v}=\frac{2��m}{qB}$
�պô���Բ�ɳ�ʱ�������ڴų����˶���ʱ�������켣Բ����Ӧ��Բ�Ľ�Ϊ��=$\frac{3��}{4}$
�����Բ�ɳ��ų��������ڴų����˶���ʱ��t1��$\frac{\frac{3��}{4}}{2��}T$����0��t1��$\frac{3��m}{4qB}$
��3�������ӵ�һ�γ��ų��Ƿ�����Բ������켣Բ������Բ�ĽǷ�ΧΪ���У��ȣ�$\frac{3}{2}$��
������Բ�������ڴų����˶���ʱ��t2���㣺$\frac{T}{2}$��t2��$\frac{\frac{3��}{2}}{2��}T$
�ã�$\frac{��m}{qB}$��t2��$\frac{3��m}{2qB}$
�𣺣�1��������Ӵ���Բ�ɳ��ų������ӵ��ٶȴ�С��Χ$v��\frac{qBR}{m}$��
��2��������Ӵ���Բ�ɳ��ų�����Щ�����ڴų����˶���ʱ�䷶Χ$0��{t}_{1}^{\;}��\frac{3��m}{4qB}$��
��3��������ӵ�һ�γ��ų��Ƿ�����Բ����Щ���Ӵӽ���ų�����һ�γ��ų����õ�ʱ�䷶Χ$\frac{��m}{qB}��{t}_{2}^{\;}��\frac{3��m}{2qB}$
���� ���⿼����������ڴų����糡�е��˶���Ҫע����ȷ�����������̣���ȷ���������ڴų��е�Բ���˶������Ӧ�ü��ι�ϵ��⣬ע�����ӵ������˶���

 �ڣ��ⶨ�����������ʣ�ʵ��ʱ������˵����ȷ���ǣ�������
�ڣ��ⶨ�����������ʣ�ʵ��ʱ������˵����ȷ���ǣ�������| A�� | ��ʵ�����ѡ�����������ƽ�еIJ���ש | |
| B�� | ���ж��ƽ�в���ש��ѡ�ã�Ӧѡ����ƽ���������������һ�� | |
| C�� | ȷ�����䡢��������ϵ���ö��ͷ��䣨P1��P2�䣬P3��P4�䣩�ľ���Ӧ������ | |
| D�� | ��ijͬѧ��ƽ�в���ש��ʵ��ʱ��ֽ������ȷ��������ש����������ab��cd�������˲���ש��ʹ����ab����ƽ����һЩ����ͼ��ʾ��������������ȷ�����������nֵ������Ӱ�� |
 һ���������Ϊ-q������Ϊm��С��ӹ⻬��Ե��б������A���ɾ�ֹ�»���С��ǡ��ͨ���뾶ΪR����ֱԲ�ι������ߵ�B����Բ���˶���������ֱ�����ϼ���ͼ��ʾ����ǿ�糡���ҵ糡ǿ������mg=2qE�����Դ�A���ɾ�ֹ�ͷŸ�С��������
һ���������Ϊ-q������Ϊm��С��ӹ⻬��Ե��б������A���ɾ�ֹ�»���С��ǡ��ͨ���뾶ΪR����ֱԲ�ι������ߵ�B����Բ���˶���������ֱ�����ϼ���ͼ��ʾ����ǿ�糡���ҵ糡ǿ������mg=2qE�����Դ�A���ɾ�ֹ�ͷŸ�С��������| A�� | С����ǡ�ù�B�� | |
| B�� | С���ܹ�B�� | |
| C�� | С���ܹ�B�㣬����B������֮��ѹ����Ϊ0 | |
| D�� | ����˵�������� |
 ijͬѧ��������ש�������ʣ������������ģ�����ʡ�ֱ�ߡ��̶ȳߡ�һ����з���Ĥ��ƽ�в���ש����ͼ��ʾ��ֱ���벣��שƽ�з��ã�����ʷ�����һ�������ֱ����O��������ש���棬��ֱ���Ϲ۲쵽A��B������㣬����OA��ľ���Ϊx1��AB��ľ���Ϊx2�����ͼ��ֱ�ߵ�����ש�ϱ������d1������ש���d2����ɼ����������������n������������벣��ש����ļнǣ����������õ������ʲ��䣨ѡ����������䡱��С���������ʵ�����к��Ϊd2��d3�����鲣��ש����֪d2��d3��Ϊ��С��������ѡ����Ϊd3��ѡ�d2����d3�����IJ���ש��
ijͬѧ��������ש�������ʣ������������ģ�����ʡ�ֱ�ߡ��̶ȳߡ�һ����з���Ĥ��ƽ�в���ש����ͼ��ʾ��ֱ���벣��שƽ�з��ã�����ʷ�����һ�������ֱ����O��������ש���棬��ֱ���Ϲ۲쵽A��B������㣬����OA��ľ���Ϊx1��AB��ľ���Ϊx2�����ͼ��ֱ�ߵ�����ש�ϱ������d1������ש���d2����ɼ����������������n������������벣��ש����ļнǣ����������õ������ʲ��䣨ѡ����������䡱��С���������ʵ�����к��Ϊd2��d3�����鲣��ש����֪d2��d3��Ϊ��С��������ѡ����Ϊd3��ѡ�d2����d3�����IJ���ש��
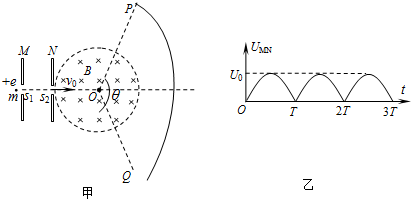 ��ͼ����ʾ��������ͬ��ƽ�н�����M��N�����ŷ��ã����Ϊ$\frac{R}{2}$����M��N�ϵ�С��s1��s2�� O���㹲�ߣ�s2O=R������s1O��ֱ�ڰ�M��N����OΪԲ�ġ�RΪ�뾶��Բ�������ڴ��ڴŸ�Ӧǿ�ȴ�СΪB������ֱֽ���������ǿ�ų����ռ���PQ�ϸ��㵽O��ľ��붼Ϊ2R�����˵�P��Q��������s1O�Գƣ���PQ���Ե�Բ�ĽǦ�=120�㣮����Ϊm�������Ϊe�������������ϵؾ�s1����M��N��ĵ糡������ͨ��s2����ų����������������Ӽ������þ����ƣ�������s1�����ٶȿ����㣮
��ͼ����ʾ��������ͬ��ƽ�н�����M��N�����ŷ��ã����Ϊ$\frac{R}{2}$����M��N�ϵ�С��s1��s2�� O���㹲�ߣ�s2O=R������s1O��ֱ�ڰ�M��N����OΪԲ�ġ�RΪ�뾶��Բ�������ڴ��ڴŸ�Ӧǿ�ȴ�СΪB������ֱֽ���������ǿ�ų����ռ���PQ�ϸ��㵽O��ľ��붼Ϊ2R�����˵�P��Q��������s1O�Գƣ���PQ���Ե�Բ�ĽǦ�=120�㣮����Ϊm�������Ϊe�������������ϵؾ�s1����M��N��ĵ糡������ͨ��s2����ų����������������Ӽ������þ����ƣ�������s1�����ٶȿ����㣮 ��ͼ��������������ȣ��ֱ�����磬������ʹ������С���ϡ��´���ƽ�н�������P������ͬ���ʴ�ֱ�糡��������糡�����Ƿֱ��䵽A��B��C���㣬������
��ͼ��������������ȣ��ֱ�����磬������ʹ������С���ϡ��´���ƽ�н�������P������ͬ���ʴ�ֱ�糡��������糡�����Ƿֱ��䵽A��B��C���㣬������