题目内容
7.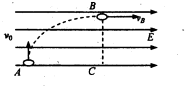 如图,一质量为m,电量+q的小球,以垂直于电场方向的速度v0竖直向上进入一个匀强电场,经过一段时间后,该小球的速度vB恰好与场强方向平行.若在此过程中水平位移是上升高度的2倍,即AC=2BC,则A、C两点间的电压是( )
如图,一质量为m,电量+q的小球,以垂直于电场方向的速度v0竖直向上进入一个匀强电场,经过一段时间后,该小球的速度vB恰好与场强方向平行.若在此过程中水平位移是上升高度的2倍,即AC=2BC,则A、C两点间的电压是( )| A. | $\frac{{mv}_{0}^2}{2q}$ | B. | $\frac{{2mv}_{0}^2}{q}$ | C. | $\frac{{mv}_{0}^2}{q}$ | D. | $\frac{{mv}_{0}^2}{4q}$ |
分析 带电粒子在重力与电场力共同作用下,从A点到B点过程中,运用运动的分解法研究:竖直方向做竖直上抛运动,水平方向做初速度为零的匀加速直线运动.根据分位移公式分别列式,抓住分运动的同时性,可知粒子到达B点时的速度,由竖直上抛运动的规律求出BC,再根据埇定理求A、C两点间的电压.
解答 解:带电粒子在重力与电场力共同作用下,从A点到B点过程中,竖直方向做竖直上抛运动,水平方向做初速度为零的匀加速直线运动,设运动时间为t,粒子到达B点时的速度为vB.则:
AC=$\frac{{v}_{B}}{2}t$,BC=$\frac{{v}_{0}}{2}t$
由于AC=2BC,
则得:vB=2v0.
由竖直上抛运动的规律得:BC=$\frac{{v}_{0}^{2}}{2g}$
根据动能定理得:qUAB-mg•BC=$\frac{1}{2}m{v}_{B}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
A、C两点间的电压 UAC=UAB,
解得 UAC=$\frac{2m{v}_{0}^{2}}{q}$
故选:B
点评 本题考查了运动如何分解,要知道当带电粒子所受的力是恒力可以考虑运用运动的分解法研究,分析时抓住分运动的等时性,运用运动学公式、牛顿第二定律、动能定理分方向列式.

练习册系列答案
相关题目
19. 在<测定玻璃的折射率>实验时,下列说法正确的是( )
在<测定玻璃的折射率>实验时,下列说法正确的是( )
 在<测定玻璃的折射率>实验时,下列说法正确的是( )
在<测定玻璃的折射率>实验时,下列说法正确的是( )| A. | 本实验必须选用两折射面相互平行的玻璃砖 | |
| B. | 若有多块平行玻璃砖可选用,应选择两平行折射面距离最大的一块 | |
| C. | 确定入射、出射光线上的两枚大头针间(P1、P2间,P3、P4间)的距离应尽量大 | |
| D. | 若某同学用平行玻璃砖做实验时在纸上已正确画出玻璃砖的两个界面ab和cd后,不慎碰了玻璃砖,使它向ab方向平移了一些,如图所示,伹其后操作都正确,则所测出的n值将不受影响 |
17. 小张和小王分别驾车沿平直公路同向行驶,在某段时间内两车的v-t图象如图所示,初始时,小张在小王前方x0处( )
小张和小王分别驾车沿平直公路同向行驶,在某段时间内两车的v-t图象如图所示,初始时,小张在小王前方x0处( )
 小张和小王分别驾车沿平直公路同向行驶,在某段时间内两车的v-t图象如图所示,初始时,小张在小王前方x0处( )
小张和小王分别驾车沿平直公路同向行驶,在某段时间内两车的v-t图象如图所示,初始时,小张在小王前方x0处( )| A. | 若x0=54 m,两车相遇1次 | B. | 若x0=36 m,两车相遇1次 | ||
| C. | 若x0=10 m,两车相遇1次 | D. | 若x0<18 m,两车相遇2次 |



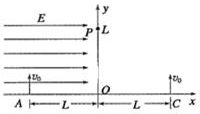 为了观察正、负电子的碰撞现象,有人设想利用电场、磁场控制正、负电子在云室中运动来实现这一过程.在如图所示的xOy平面内,A、C二小孔距原点的距离均为L,每隔一定的时间源源不断地分别从A孔射入正电子,C孔射入负电子,初速度均为v0,且垂直x轴,正、负电子的质量均为m,电荷量均为e(忽略电子之间的相互作用).在y轴的左侧区域加一水平向右的匀强电场,在y轴的右侧区域加一垂直纸面的匀强磁场(图中未画出),要使正、负电子在y轴上的P(0,L)处相碰,求:
为了观察正、负电子的碰撞现象,有人设想利用电场、磁场控制正、负电子在云室中运动来实现这一过程.在如图所示的xOy平面内,A、C二小孔距原点的距离均为L,每隔一定的时间源源不断地分别从A孔射入正电子,C孔射入负电子,初速度均为v0,且垂直x轴,正、负电子的质量均为m,电荷量均为e(忽略电子之间的相互作用).在y轴的左侧区域加一水平向右的匀强电场,在y轴的右侧区域加一垂直纸面的匀强磁场(图中未画出),要使正、负电子在y轴上的P(0,L)处相碰,求:
 如图所示,在MN右侧有一个磁感应强度B=0.50T的匀强磁场.在磁场中的A点有一静止镭核(${\;}_{88}^{236}$Ra),A点距MN的距离OA=1.0m.D为放置在MN边缘的粒子接收器,OD=1.0m.${\;}_{88}^{236}$Ra发生衰变时,放出某粒子x后变为一氡核(${\;}_{86}^{222}$Rn),接收器D恰好接收到了沿垂直于MN方向射来的粒子x.(近似计算时,可认为核的质量等于质量数乘以原子质量u,1u=1.7×10-27kg.元电荷e=1.6×10-19C).(注:本题计算结果都保留二位有效数字)
如图所示,在MN右侧有一个磁感应强度B=0.50T的匀强磁场.在磁场中的A点有一静止镭核(${\;}_{88}^{236}$Ra),A点距MN的距离OA=1.0m.D为放置在MN边缘的粒子接收器,OD=1.0m.${\;}_{88}^{236}$Ra发生衰变时,放出某粒子x后变为一氡核(${\;}_{86}^{222}$Rn),接收器D恰好接收到了沿垂直于MN方向射来的粒子x.(近似计算时,可认为核的质量等于质量数乘以原子质量u,1u=1.7×10-27kg.元电荷e=1.6×10-19C).(注:本题计算结果都保留二位有效数字)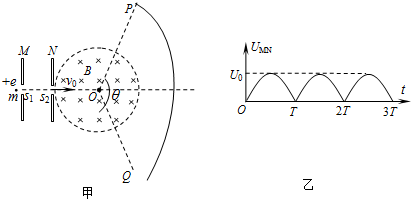 如图甲所示,两块相同的平行金属板M、N正对着放置,相距为$\frac{R}{2}$,板M、N上的小孔s1、s2与 O三点共线,s2O=R,连线s1O垂直于板M、N.以O为圆心、R为半径的圆形区域内存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场.收集屏PQ上各点到O点的距离都为2R,两端点P、Q关于连线s1O对称,屏PQ所对的圆心角θ=120°.质量为m、电荷量为e的质子连续不断地经s1进入M、N间的电场,接着通过s2进入磁场.质子重力及质子间的相互作用均不计,质子在s1处的速度看作零.
如图甲所示,两块相同的平行金属板M、N正对着放置,相距为$\frac{R}{2}$,板M、N上的小孔s1、s2与 O三点共线,s2O=R,连线s1O垂直于板M、N.以O为圆心、R为半径的圆形区域内存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场.收集屏PQ上各点到O点的距离都为2R,两端点P、Q关于连线s1O对称,屏PQ所对的圆心角θ=120°.质量为m、电荷量为e的质子连续不断地经s1进入M、N间的电场,接着通过s2进入磁场.质子重力及质子间的相互作用均不计,质子在s1处的速度看作零.