题目内容
14. 如图所示,在一个倾角为θ的固定斜面上,让小木块从静止开始匀加速滑下.测得小木块在时间t内通过的位移为x,已知重力加速度为g,求:
如图所示,在一个倾角为θ的固定斜面上,让小木块从静止开始匀加速滑下.测得小木块在时间t内通过的位移为x,已知重力加速度为g,求:(1)小木块在下滑过程中的加速度a
(2)小木块与斜面间的摩擦因素?.
分析 (1)物体由静止匀加速下滑,已知位移为x,时间为t,根据运动学公式x=$\frac{1}{2}$at2,求出加速度;
(2)根据牛顿第二定律,求出合力,通过受力分析,求出摩擦力和支持力,再根据f=μN,求动摩擦因数.
解答 解:(1)物体由静止匀加速下滑,已知位移为x,时间为t,由x=$\frac{1}{2}$at2得加速度为:a=$\frac{2x}{{t}^{2}}$.
(2)根据牛顿第二定律得:F合=ma
对物体进行受力分析,运用正交分解得:N=mgcosθ
则得:mgsinθ-f=ma,
f=mgsinθ-ma
所以有:μ=$\frac{f}{N}$=$\frac{mgsinθ-m•\frac{2x}{{t}^{2}}}{mgcosθ}$=$\frac{gsinθ-\frac{2x}{{t}^{2}}}{gcosθ}$.
答:(1)小木块在下滑过程中的加速度a是$\frac{2x}{{t}^{2}}$;
(2)小木块与斜面间的动摩擦因数μ是$\frac{gsinθ-\frac{2x}{{t}^{2}}}{gcosθ}$.
点评 本题属于根据运动求力,联系前后的桥梁是加速度.根据运动学公式求出加速度,根据牛顿第二定律求出合力,从而求出未知力.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
5.下列所述的实例中,机械能守恒的是( )
| A. | 小钢球在空中做平抛运动的过程 | B. | 人乘电梯加速上升的过程 | ||
| C. | 木箱沿斜面匀速向下滑行的过程 | D. | 跳伞运动员在空中匀速下落的过程 |
19. 水平平行放置的金属板a、b间加上恒定电压,两板间距离为d.一带电粒子紧贴a板水平射入电场,刚好紧贴b板射出,如图所示.在其他条件不变的情况下,若将b板向下平移一段距离x,带电粒子刚好从两板中央射出.不考虑重力的影响,则( )
水平平行放置的金属板a、b间加上恒定电压,两板间距离为d.一带电粒子紧贴a板水平射入电场,刚好紧贴b板射出,如图所示.在其他条件不变的情况下,若将b板向下平移一段距离x,带电粒子刚好从两板中央射出.不考虑重力的影响,则( )
 水平平行放置的金属板a、b间加上恒定电压,两板间距离为d.一带电粒子紧贴a板水平射入电场,刚好紧贴b板射出,如图所示.在其他条件不变的情况下,若将b板向下平移一段距离x,带电粒子刚好从两板中央射出.不考虑重力的影响,则( )
水平平行放置的金属板a、b间加上恒定电压,两板间距离为d.一带电粒子紧贴a板水平射入电场,刚好紧贴b板射出,如图所示.在其他条件不变的情况下,若将b板向下平移一段距离x,带电粒子刚好从两板中央射出.不考虑重力的影响,则( )| A. | x=d | B. | x=$\frac{1}{2}$d | C. | x=$\sqrt{2}$d | D. | x=($\sqrt{2}-1$)d |
6.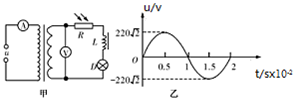 如图甲所示的电路中,理想变压器原、副线圈匝数比为10:1,A、V均为理想电表,R、L和D分别是光敏电阻(其阻值随光强增大而减小)、理想线圈和灯泡.原线圈接入如图乙所示的正弦交流电压u,下列说法正确的是( )
如图甲所示的电路中,理想变压器原、副线圈匝数比为10:1,A、V均为理想电表,R、L和D分别是光敏电阻(其阻值随光强增大而减小)、理想线圈和灯泡.原线圈接入如图乙所示的正弦交流电压u,下列说法正确的是( )
 如图甲所示的电路中,理想变压器原、副线圈匝数比为10:1,A、V均为理想电表,R、L和D分别是光敏电阻(其阻值随光强增大而减小)、理想线圈和灯泡.原线圈接入如图乙所示的正弦交流电压u,下列说法正确的是( )
如图甲所示的电路中,理想变压器原、副线圈匝数比为10:1,A、V均为理想电表,R、L和D分别是光敏电阻(其阻值随光强增大而减小)、理想线圈和灯泡.原线圈接入如图乙所示的正弦交流电压u,下列说法正确的是( )| A. | 电压u的频率为100 Hz | B. | V的示数为22$\sqrt{2}$V | ||
| C. | 有光照射R时,A的示数变大 | D. | 抽出L中的铁芯,D变暗 |
3. 如图所示,匀强磁场的磁感应强度大小为B.匝数为N、面积为S的矩形线圈绕垂直于磁场的轴OO′以角速度ω匀速转动,不计线圈电阻.线圈通过电刷与一理想变压器原线圈相接,变压器的原、副线圈的匝数分别为n1、n2.A为理想交流电流表.L1、L2为两个完全相同的电灯泡,标称值为“U0,P0”,且当S闭合时两灯泡均正常发光.除灯泡电阻外,不计其它电阻.则以下说法正确的是( )
如图所示,匀强磁场的磁感应强度大小为B.匝数为N、面积为S的矩形线圈绕垂直于磁场的轴OO′以角速度ω匀速转动,不计线圈电阻.线圈通过电刷与一理想变压器原线圈相接,变压器的原、副线圈的匝数分别为n1、n2.A为理想交流电流表.L1、L2为两个完全相同的电灯泡,标称值为“U0,P0”,且当S闭合时两灯泡均正常发光.除灯泡电阻外,不计其它电阻.则以下说法正确的是( )
 如图所示,匀强磁场的磁感应强度大小为B.匝数为N、面积为S的矩形线圈绕垂直于磁场的轴OO′以角速度ω匀速转动,不计线圈电阻.线圈通过电刷与一理想变压器原线圈相接,变压器的原、副线圈的匝数分别为n1、n2.A为理想交流电流表.L1、L2为两个完全相同的电灯泡,标称值为“U0,P0”,且当S闭合时两灯泡均正常发光.除灯泡电阻外,不计其它电阻.则以下说法正确的是( )
如图所示,匀强磁场的磁感应强度大小为B.匝数为N、面积为S的矩形线圈绕垂直于磁场的轴OO′以角速度ω匀速转动,不计线圈电阻.线圈通过电刷与一理想变压器原线圈相接,变压器的原、副线圈的匝数分别为n1、n2.A为理想交流电流表.L1、L2为两个完全相同的电灯泡,标称值为“U0,P0”,且当S闭合时两灯泡均正常发光.除灯泡电阻外,不计其它电阻.则以下说法正确的是( )| A. | 从图示位置开始计时,线框内产生的交变电流的电动势随时间的瞬时值表达式为e=NBSωcosωt | |
| B. | 理想变压器原副线圈的匝数比为$\frac{{n}_{1}}{{n}_{2}}$=$\frac{NBSω}{\sqrt{2}{U}_{0}}$ | |
| C. | 当S断开后,L1比断开前暗 | |
| D. | 当S断开后,电流表的示数比断开前大 |
4. 如图所示,空间存在垂直纸面的匀强磁场,在半径为a的圆形区域内外的磁场方向相反,磁感应强度的大小均为B0.一半径为b、电阻为R的圆形导线环放置在纸面内.其圆心与圆形区域的中心重合,外接电阻的阻值也为R.在时间t内,两匀强磁场同时由B0均匀减小到0,在此过程中,下列说法正确的是( )
如图所示,空间存在垂直纸面的匀强磁场,在半径为a的圆形区域内外的磁场方向相反,磁感应强度的大小均为B0.一半径为b、电阻为R的圆形导线环放置在纸面内.其圆心与圆形区域的中心重合,外接电阻的阻值也为R.在时间t内,两匀强磁场同时由B0均匀减小到0,在此过程中,下列说法正确的是( )
 如图所示,空间存在垂直纸面的匀强磁场,在半径为a的圆形区域内外的磁场方向相反,磁感应强度的大小均为B0.一半径为b、电阻为R的圆形导线环放置在纸面内.其圆心与圆形区域的中心重合,外接电阻的阻值也为R.在时间t内,两匀强磁场同时由B0均匀减小到0,在此过程中,下列说法正确的是( )
如图所示,空间存在垂直纸面的匀强磁场,在半径为a的圆形区域内外的磁场方向相反,磁感应强度的大小均为B0.一半径为b、电阻为R的圆形导线环放置在纸面内.其圆心与圆形区域的中心重合,外接电阻的阻值也为R.在时间t内,两匀强磁场同时由B0均匀减小到0,在此过程中,下列说法正确的是( )| A. | 电路中产生的感应电动势为$\frac{π{B}_{0}|{b}^{2}-2{a}^{2}|}{t}$ | |
| B. | 电路中产生的感应电动势为$\frac{π{B}_{0}|{b}^{2}-{a}^{2}|}{t}$ | |
| C. | 通过R的电荷量为$\frac{π{B}_{0}({b}^{2}-{a}^{2})}{R}$ | |
| D. | 通过R的电荷量为$\frac{π{B}_{0}|{b}^{2}-2{a}^{2}|}{2R}$ |
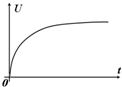
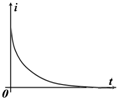
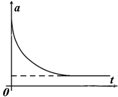
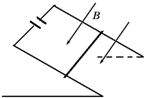 如图,两足够长的光滑平行金属导轨倾斜放置,导轨左端接有耐压足够的电容器C,匀强磁场B垂直导轨平面,有一导体棒垂直导轨和磁场放置,可紧贴导轨自由滑动,导体棒和导轨电阻忽略不计.现导体棒由静止释放,电容器两端电压为U,导体棒加速度为a、通过的电流为i、重力功率为P,则下列图象能正确反映各量随时间变化规律的是:( )
如图,两足够长的光滑平行金属导轨倾斜放置,导轨左端接有耐压足够的电容器C,匀强磁场B垂直导轨平面,有一导体棒垂直导轨和磁场放置,可紧贴导轨自由滑动,导体棒和导轨电阻忽略不计.现导体棒由静止释放,电容器两端电压为U,导体棒加速度为a、通过的电流为i、重力功率为P,则下列图象能正确反映各量随时间变化规律的是:( )