��Ŀ����
11����ͼ��ʾ��������Ϊm�����A��B���ᵯ�����������ڹ⻬��б���ϣ�б�����Ǧ�=30�㣬B��б��˵Ĺ̶�����Ӵ������ɵľ���ϵ��Ϊk��Aͨ��һ���ƹ������IJ����쳤�����������ˮƽ���ϵ����C�����������������ڸպ���ֱ״̬��A�϶�����б��ƽ�У�C�������ˮƽ��ƽ�У�C������ҲΪm��б���㹻�������C��ˮƽ���Ķ�Ħ������Ϊ��=0.5���������ٶ�Ϊg���ָ�C��һ�����ҵij��ٶȣ���C�����˶����ٶ�Ϊ��ʱ��B�պ�Ҫ�뿪���壬��
��1�����C��ʼ�����˶��ij��ٶȴ�С��
��2������Cʩ��һ�����ҵ�ˮƽ����F1��δ֪��ʹC�����˶�����B�պ�Ҫ�뿪����ʱ�����A���ٶȴ�СΪv��������F1���
��3������Cһ�����ҵ�ˮƽ����F2��δ֪��ʹC�����˶�����B�պ�Ҫ�뿪����ʱ�����A�ļ��ٶȴ�СΪa����ʱ����F2���Ĺ��Ƕ��٣�
���� ��1���ȷ������ɵij�ĩ״̬���жϳ��˹����е��ɵ������ܵı仯��Ϊ�㣬��A��C��������ɵ�ϵͳ�����û�е���غ㶨����ʽ������������C��ʼ�����˶��ij��ٶȴ�С��
��2���ȸ��ݺ��˶��ɺͼ��ι�ϵ���A�ϻ��ľ��룬�ٶ�A��C��������ɵ�ϵͳ�����ù���ԭ��������F1��
��3����A��C�ֱ�����ţ�ٵڶ�������ʽ���������F2�����ɹ��ļ��㹫ʽ������F2���Ĺ���
��� �⣺��1������ԭ����ѹ����Ϊ��
x1=$\frac{mgsin��}{k}$=$\frac{mg}{2k}$
B�պ�Ҫ�뿪����ʱ���ɵ��쳤��Ϊ��
x2=$\frac{mgsin��}{k}$=$\frac{mg}{2k}$
����x1=x2��
���Գ�ĩ״̬���ɵĵ���������ȣ���A��C��������ɵ�ϵͳ�����û�е���غ㶨�ɵã�
2��$\frac{1}{2}m{v}_{0}^{2}$=mgsin��•��x1+x2��
���C�ij��ٶ�Ϊ��v0=$\sqrt{\frac{m{g}^{2}}{2k}}$
��2��A�ϻ��ľ���Ϊ��s=x1+x2=$\frac{mg}{k}$
��A��C��������ɵ�ϵͳ�����ù���ԭ���ã�
F1s=mgsin��•s+2��$\frac{1}{2}m{v}^{2}$
�ɵã�F1=$\frac{1}{2}$mg+$\frac{k{v}^{2}}{g}$
��3����B�պ�Ҫ�뿪����ʱ����ţ�ٵڶ����ɵã�
��A��T-mgsin��-kx2=ma
��C��F2-T=ma
����F2���Ĺ�Ϊ��W=F2s
������ã�W=$\frac{{m}^{2}g��g+2a��}{k}$
�𣺣�1�����C��ʼ�����˶��ij��ٶȴ�С��$\sqrt{\frac{m{g}^{2}}{2k}}$��
��2������F1Ϊ$\frac{1}{2}$mg+$\frac{k{v}^{2}}{g}$��
��3����ʱ����F2���Ĺ���$\frac{{m}^{2}g��g+2a��}{k}$��
���� ���������������⣬ҪץסA��C���ٶȴ�С��ȡ����ٶȴ�С��ȣ�Ҫ���ѡ���о������ø��뷨�����巨���ϵķ����о����ܹ�ϵ��������ٶȵĹ�ϵ��

 ��ͼ��ʾ������Ϊ3m��������һ����Ϊm���߿���һ����Եϸ���������������������߶���ͬ�Ķ������ϣ���֪�߿����ΪR����߱߳�ΪL��ˮƽ������ǿ�ų��ĴŸ�Ӧǿ��ΪB���ų����±߽�ľ��롢�߿���ֱ�߳���Ϊh����ʼʱ�̣��ų����±�Ե���߿��ϱ�Ե�ĸ߶Ȳ�Ϊ2h��������Ӿ�ֹ��ʼ�ͷţ��߿��ų�ǰ�����߿��Ѿ�������ֱ���˶�������������Ħ�����������ƣ�������˵������ȷ���ǣ�������
��ͼ��ʾ������Ϊ3m��������һ����Ϊm���߿���һ����Եϸ���������������������߶���ͬ�Ķ������ϣ���֪�߿����ΪR����߱߳�ΪL��ˮƽ������ǿ�ų��ĴŸ�Ӧǿ��ΪB���ų����±߽�ľ��롢�߿���ֱ�߳���Ϊh����ʼʱ�̣��ų����±�Ե���߿��ϱ�Ե�ĸ߶Ȳ�Ϊ2h��������Ӿ�ֹ��ʼ�ͷţ��߿��ų�ǰ�����߿��Ѿ�������ֱ���˶�������������Ħ�����������ƣ�������˵������ȷ���ǣ�������| A�� | �߿����ų�ʱ���ٶ�Ϊ$\sqrt{gh}$ | |
| B�� | �߿��ų�ʱ���ٶ�Ϊ$\frac{mgR}{{B}^{2}{L}^{2}}$ | |
| C�� | �߿�ͨ���ų��Ĺ����в���������Q=8mgh-$\frac{8{m}^{3}{g}^{2}{R}^{2}}{{B}^{4}{L}^{4}}$ | |
| D�� | �߿����ų�����ijһʱ�̵��ٶ�Ϊv������ٶ�Ϊa=$\frac{1}{2}$g-$\frac{{B}^{2}{L}^{2}v}{4mR}$ |
 ���϶���š����·��еĸ߶�Ϊ100km����̽����й���������ݽ��Ȼ��·��и߶�Ϊ200km�ġ��϶�һ�š�������ʵ�����������ǻ��µ����о�����Ϊ����Բ���˶������й����ͼ��ʾ��������
���϶���š����·��еĸ߶�Ϊ100km����̽����й���������ݽ��Ȼ��·��и߶�Ϊ200km�ġ��϶�һ�š�������ʵ�����������ǻ��µ����о�����Ϊ����Բ���˶������й����ͼ��ʾ��������| A�� | ���϶���š��������е����ڱȡ��϶�һ�š�С | |
| B�� | ���϶���š��������е����ٶȱȡ��϶�һ�š�С | |
| C�� | ���϶���š��������е����ļ��ٶȱȡ��϶�һ�š��� | |
| D�� | ���϶���š��������е��������롰�϶�һ�š���� |
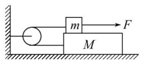 ��ͼ��ʾ��ľ������ΪM������ΪL��Сľ�飨����Ϊ�ʵ㣩������Ϊm��ˮƽ����⻬��һ����������������ͨ�������ֱַ���ľ���Сľ�����ӣ�Сľ����ľ���Ķ�Ħ������Ϊ�̣���ʼʱľ�龲ֹ��ľ����ˣ�����ˮƽ���ҵ�����Сľ������ľ���Ҷˣ�������������Ϊ��������
��ͼ��ʾ��ľ������ΪM������ΪL��Сľ�飨����Ϊ�ʵ㣩������Ϊm��ˮƽ����⻬��һ����������������ͨ�������ֱַ���ľ���Сľ�����ӣ�Сľ����ľ���Ķ�Ħ������Ϊ�̣���ʼʱľ�龲ֹ��ľ����ˣ�����ˮƽ���ҵ�����Сľ������ľ���Ҷˣ�������������Ϊ��������| A�� | 2��mgL | B�� | ��mgL | C�� | �̣�M+m��gL | D�� | $\frac{��mgL}{2}$ |
 ��ͼ1��ʾ�����Ϊ37����㹻���Ĵ��ʹ��Ժ㶨�ٶ����У���һ����m=1kg��С������ijһ���ٶȷ��ϴ��ʹ���������Ե�����ٶȴ�С��ʱ��仯�Ĺ�ϵ��ͼ2��ʾ��ȡ�ش��ʹ�����Ϊ������g=10m/s2��sin37��=0.6��cos37��=0.8��������˵����ȷ���ǣ�������
��ͼ1��ʾ�����Ϊ37����㹻���Ĵ��ʹ��Ժ㶨�ٶ����У���һ����m=1kg��С������ijһ���ٶȷ��ϴ��ʹ���������Ե�����ٶȴ�С��ʱ��仯�Ĺ�ϵ��ͼ2��ʾ��ȡ�ش��ʹ�����Ϊ������g=10m/s2��sin37��=0.6��cos37��=0.8��������˵����ȷ���ǣ�������| A�� | �����봫�ʹ���Ķ�Ħ������Ϊ0.75 | |
| B�� | 0��8s������λ�ƵĴ�СΪ14m | |
| C�� | 0��8s�������е�ܵ�����Ϊ84J | |
| D�� | 0��8s�������봫�ʹ�֮����Ħ��������������Ϊ126J |
 ��ͼ��ʾ������ƽ�е�ˮƽ�����������L=1m�������������б������ˮƽ����ļн�Ϊ37�㣬����װ�ô�����ֱ���µ���ǿ�ų��У�������PQ������Ϊm=0.2kg��MN��PQ����ֱ�ΪR1=1����R2=2����MN���ڴֲ�ˮƽ�����ϣ�PQ���ڹ⻬����б�����ϣ��������������뵼�촹ֱ�ҽӴ����ã�MN����ˮƽ����F1����������v1=3m/s���ٶ�����������ֱ���˶���PQ����ƽ����б�淽�����F2�����±��־�ֹ״̬����ʱPQNM��·���ĵĵ繦��ΪP=3W�����Ƶ���ĵ��裬ˮƽ�����㹻����MNʼ����ˮƽ�������˶�����sin 37��=0.6��cos 37��=0.8����
��ͼ��ʾ������ƽ�е�ˮƽ�����������L=1m�������������б������ˮƽ����ļн�Ϊ37�㣬����װ�ô�����ֱ���µ���ǿ�ų��У�������PQ������Ϊm=0.2kg��MN��PQ����ֱ�ΪR1=1����R2=2����MN���ڴֲ�ˮƽ�����ϣ�PQ���ڹ⻬����б�����ϣ��������������뵼�촹ֱ�ҽӴ����ã�MN����ˮƽ����F1����������v1=3m/s���ٶ�����������ֱ���˶���PQ����ƽ����б�淽�����F2�����±��־�ֹ״̬����ʱPQNM��·���ĵĵ繦��ΪP=3W�����Ƶ���ĵ��裬ˮƽ�����㹻����MNʼ����ˮƽ�������˶�����sin 37��=0.6��cos 37��=0.8���� ��ͼ��ʾ����ˮƽ������������������MN��PQ��������Ϊd����ǿ�ų���ֱ�ڵ������ڵ�ƽ������Ÿ�Ӧǿ�ȵĴ�СΪB������������Ϊm����ȫ��ͬ�Ľ�����1��2���һ���ľ���ڿ����ڵ����ϣ����뵼�촹ֱ�����ǵĵ����ΪR�������뵼��Ӵ����ã�������費�ƣ������˵�Ħ�����ƣ���1�Գ��ٶ�v0�����2��Ϊʹ���˲���������
��ͼ��ʾ����ˮƽ������������������MN��PQ��������Ϊd����ǿ�ų���ֱ�ڵ������ڵ�ƽ������Ÿ�Ӧǿ�ȵĴ�СΪB������������Ϊm����ȫ��ͬ�Ľ�����1��2���һ���ľ���ڿ����ڵ����ϣ����뵼�촹ֱ�����ǵĵ����ΪR�������뵼��Ӵ����ã�������費�ƣ������˵�Ħ�����ƣ���1�Գ��ٶ�v0�����2��Ϊʹ���˲���������